10.5 연결 성분
연결 성분(connected component): 최대로 연결된 부분 그래프
1. 그래프 상의 임의의 정점을 선택해 깊이 우선 탐색이나 너비 우선 탐색을 시작하면 시작 정점으로부터 도달 가능한 모든 정점들이 하나의 연결 성분이 됨
2. 다음에 방문 안된 정점을 선택해서 다시 탐색을 실행하면 그 정점을 포함하는 연결 성분이 구해짐
3. 그래프 상의 모든 정점이 방문될 때가지 이 과정을 되풀이하면 그래프에 존재하는 모든 연결 성분들을 찾을 수 있음
<프로그램 10.5.1> 연결 성분 프로그램
void find_connected_component(GraphType *g){
count = 0;
for(int i=0; i<g->n;i++){
if(!visited[i]){ // 방문되지 않았으면
count++;
dfs_mat(g,i);
}
}
}
10.6 신장 트리
신장 트리(spanning tree): 그래프 내의 모든 정점을 포함하는 트리
- 트리의 특수한 형태이므로 모든 정점들이 연결되어 있어야 하고, 사이클을 포함해서는 안됨
- 따라서, 신장 트리의 그래프에 있는 n개의 정점을 정확히 (n-1)개의 간선으로 연결하게 됨
-> 신장 트리는 그래프의 최소 연결 부분 그래프가 됨, 최소의 의미: 간선의 수가 가장 적다는 의미

깊이 우선 신장 트리: 맨 왼쪽 신장 트리, 시작 정점 0으로 깊이 우선 탐색할 때 사용된 간선으로만 만들어진 신장 트리
너비 우선 신장 트리: 중간 신장 트리, 시작 정점 0으로 너비 우선 탐색할 때 사용된 간선으로만 만들어진 신장 트리
<알고리즘 10.6.1> 신장 트리 알고리즘
depth_first_search(v)
v를 방문되었다고 표시;
for all u ∈ (v에 인접한 정점) do
if (u가 아직 방문되지 않았으면)
then (v,u)를 신장 트리 간선이라고 표시
depth_first_search(u)10.7 최소 비용 신장 트리
최소 비용 신장 트리(MST: minimum spanning tree): 신장 트리 중에서 사용된 간선들의 가중치 합이 최소인 신장 트리
- 도로 건설: 도시들을 모두 연결하면서 도로의 길이가 최소가 되도록 하는 문제
- 전기 회로: 단자들을 모두 연결하면서 전선의 길이가 가장 최소가 되도록 하는 문제
- 통신: 전화선의 길이가 최소가 되도록 전화 케이블 망을 구성하는 문제
- 배관: 파이프를 모두 연결하면서 파이프의 총 길이가 최소가 되도록 연결하는 문제
최소 신장 트리 구하는 방법
-> Kruskal, Prim이 제안한 알고리즘
-> 최소 비용 신장 트리가 간선의 가중치의 합이 최소여야함
-> 반드시 (n-1)개의 간선만 사용해야 함
-> 사이클이 포함되어서는 안됨
10.7.1 Kruskal의 MST 알고리즘
Kruskal 알고리즘
- 탐욕적인 방법(greedy method)을 이용함 -> 결정을 해야할 때마다 그 순간에 가장 좋다고 생각되는 것을 해답으로 선택함으로써 최종적인 해답에 도달
- 그 순간의 선택은 그 당시에는 최적임, 그러나 최적이라고 생각했던 해답들을 모아서 최종적인 해답을 만들었다고 해서 그 해답이 전체적인 관점에서 최적이라는 보장은 없음
-> 따라서 탐욕적인 방법은 항상 최적의 해답을 주는지 반드시 검증해야 함 - 최소 비용 신장 트리가 최소 비용의 간선으로 구성됨과 동시에 사이클을 포함하지 않는다는 조건에 따라 각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택함, 이러한 과정을 반복함으로써 네트워크의 모든 정점을 최소 비용으로 연결하는 최적 해답을 구할 수 있음
- 그래프의 e개의 간선들을 가중치의 오름차순으로 정렬
- 정렬된 간선 리스트에서 순서대로 사이클을 형성 하지 않는 간선을 선택하여 현재의 최소 비용 신장 트리의 집합에 추가함
- 사이클을 형성하면 그 간선은 제외됨
<알고리즘 10.7.1.1> Kruskal 최소 비용 신장 트리 알고리즘
// 최소 비용 신장 트리를 구하는 kruskal의 알고리즘
// 입력: 가중치 그래프 G = (V, E), n은 노드의 개수
// 출력: Et, 최소 비용 신장 트리를 이루는 간선들의 집합
kruskal(G)
E를 w(e1) <= ... <= w(ee)가 되도록 정렬
Et <- Φ; ecounter <- 0
k <- 0
while ecounter < (n-1) do
k <- k + 1
if Et U {ek}가 사이클을 포함하지 않으면
then Et <- Et U {ek}; ecounter <- ecounter + 1
return Et 
사이클 생성 여부 체크
- 새로운 간선이 이미 다른 경로에 의해 연결되어 있는 정점들을 연결하는 경우 사이클 형성
- 간선의 양 끝 점이 같은 집합에 속한 경우 사이클 형성, 다른 집합에 속한 경우 사이클 형성 안됨
-> 간선의 양 끝 점이 같은 집합에 속해 있는지 검사 필요 => union-find 연산
union-find 연산
union(x,y): 원소 x와 y가 속해 있는 집합을 입력으로 받아 2개의 집합의 합집합을 만듦
- union 연산 시에 정점의 개수가 적은 트리의 루트가 큰 트리를 가리키도록 하면 좋음
find(x): 원소 x가 속해 있는 집합을 반환
- find 연산의 수행 시간을 줄이기 위해서는 특정 정점과 루트의 거리가 가까워야 함 -> 모든 정점이 루트 바로 아래 있도록 함
ex) S = {1,2,3,4,5,6}
1. 집합의 원소를 하나씩 분리하여 독자적인 집합으로 만듦
{1}, {2}, {3}, {4}, {5}, {6}
2. union(1,4), union(5,2)를 하면
{1,4}, {5,2}, {3}, {6}
3. union(4,5), union(3,6)을 하면
{1,4,5,2},{3,6}
집합을 구현하는데 여러가지 방법 존재
- 비트 벡터, 배열, 연결 리스트, 트리
<프로그램 10.7.1.1> union-find 프로그램
int parent[MAX_VERTICES]; // 부모 노드
int num[MAX_VERTICES]; // 각 집합의 크기
// 초기화
void set_init(int n){
for(int i=0;i<n;i++){
parent[i] = -1; // 루트의 정점은 부모 배열에서 -1을 가짐
num[i] = 1;
}
}
// vertex가 속하는 집합을 반환
int set_find(int vertex){
int p,s,i=-1;
for(i=vertex; (p = parent[i]) >=0;i=p){ // 루트 노드까지 반복
}
s = i; // 집합의 대표 원소
for(i=vertex;(p = parent[i]) >=0;i=p){
parent[i] = s; // 집합의 모든 원소들의 부모를 s로 설정
}
return s;
}
// 두 개의 원소가 속한 집합을 합침
void set_union(int s1, int s2){
if(num[s1] < num[s2] ){
parent[s1] = s2;
num[s2] += num[s1];
}else{
parent[s2] = s1;
num[s1] += num[s2];
}
}<프로그램 10.7.1.2> Kruskal의 최소 비용 신장 트리 프로그램
#include <stdio.h>
#define MAX_VERTICES 100
#define INF 1000
int parent[MAX_VERTICES]; // 부모 노드
int num[MAX_VERTICES]; // 각 집합의 크기
// 집합 초기화
void set_init(int n)
{
for (int i = 0; i < n; i++) {
parent[i] = -1; // 루트의 정점은 부모 배열에서 -1을 가짐
num[i] = 1;
}
}
// vertex가 속하는 집합을 반환
int set_find(int vertex)
{
int p, s, i = -1;
for (i = vertex; (p = parent[i]) >= 0; i = p) { // 루트노드까지 반복
}
s = i; // 집합의 대표 원소
for (i = vertex; (p = parent[i]) >= 0; i = p) {
parent[i] = s; // 집합의 모든 원소들의 부모를 s로 설정
}
return s;
}
// 두 개의 원소가 속한 집합을 합침
void set_union(int s1, int s2)
{
if (num[s1] < num[s2]) {
parent[s1] = s2;
num[s2] += num[s1];
} else {
parent[s2] = s1;
num[s1] += num[s2];
}
}
// 힙의 요소 타입 정의
typedef struct {
int key; // 간선의 가중치
int u; // 정점1
int v; // 정점2
} element;
#define MAX_ELEMENT 100
// 최소 힙 프로그램 - krusal에서 간선들의 가중치의 오름차순으로 정렬하기 때문
typedef struct{
element heap[MAX_ELEMENT];
int heap_size;
} HeapType;
// 힙 초기화 함수
void init(HeapType *h){
h->heap_size = 0;
}
int is_empty(HeapType*h){
if(h->heap_size == 0){
return true;
}else{
return false;
}
}
// 삽입함수
void insert_min_heap(HeapType*h, element item){
int i = ++h->heap_size;
// 트리를 거슬러 올라가면서 부모 노드와 비교
while((i != 1) && (item.key < h->heap[i/2].key)){
h->heap[i] = h->heap[i / 2];
i /= 2;
}
h->heap[i] = item; // 새로운 노드 삽입
}
// 삭제 함수
element delete_min_heap(HeapType*h){
element item = h->heap[1];
element tmp = h->heap[(h->heap_size)--];
int parent = 1;
int child = 2;
while(child <=h->heap_size){
// 현재 노드의 자식 노드 중 더 작은 자식 노드를 찾음
if((child < h->heap_size) && (h->heap[child].key > h->heap[child+1].key) ){
child++;
}
if(tmp.key <= h->heap[child].key)
break;
// 한단계 아래로 이동
h->heap[parent] = h->heap[child];
parent = child;
child *= 2;
}
h->heap[parent] = tmp;
return item;
}
// 정점u와 정점 v를 연결하는 가중치가 weight인 간선을 힙에 삽입
void insert_heap_edge(HeapType *h, int u, int v, int weight){
element e;
e.u = u;
e.v = v;
e.key = weight;
insert_min_heap(h, e);
}
// 인접행렬이나 인접리스트에서 간선들을 읽어서 최소 힙에 삽입
// 현재는 예제 그래프의 간선들을 삽입함
void insert_all_edges(HeapType *h){
insert_heap_edge(h, 0, 1, 29);
insert_heap_edge(h, 1, 2, 16);
insert_heap_edge(h, 2, 3, 12);
insert_heap_edge(h, 3, 4, 22);
insert_heap_edge(h, 4, 5, 27);
insert_heap_edge(h, 5, 0, 10);
insert_heap_edge(h, 6, 1, 15);
insert_heap_edge(h, 6, 3, 18);
insert_heap_edge(h, 6, 2, 25);
}
// kruskal의 최소 비용 신장 트리 프로그램
void kruskal(int n){
int edge_accepted = 0; // 현재까지 선택된 간선의 수
HeapType h; // 최소 힙
int uset, vset; // 정점 u와 정점 v의 집합 번호
element e; // 힙 요소
init(&h); // 힙 초기화
insert_all_edges(&h); // 힙에 간선들을 삽입
set_init(n); // 집합 초기화
while(edge_accepted < (n-1)){
e = delete_min_heap(&h); // 최소 힙에서 삭제
uset = set_find(e.u); // 정점 u의 집합 번호
vset = set_find(e.v); // 정점 v의 집합 번호
if(uset != vset){ // 서로 속한 집합이 다르면
printf("(%d %d) %d\n", e.u, e.v, e.key);
edge_accepted++;
set_union(uset, vset); // 두개의 집합을 합침
}
}
}
int main(){
kruskal(7);
}
시간복잡도
- 간선들을 정렬하는 시간에 좌우됨
- 따라서 퀵 정렬를 이용하여 간선 e를 정렬할 경우, 가 됨
10.7.2 Prim의 MST 알고리즘
Prim의 알고리즘: 시작 정점에서부터 출발하여 신장 트리 집합을 단계적으로 확장해나가는 방법
- 시작 단계에서는 시작 정점만이 신장 트리 집합에 포함됨
- 앞 단계에서 만들어진 신장 트리 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장함
- 트리가 n-1개의 간선을 가질 때까지 계속됨

Kruskal 알고리즘 = 간선 선택을 기반으로 하는 알고리즘, 이전 단계에서 만들어진 신장 트리와는 상관없이 무조건 최소 간선만을 선택하는 방법
Prim 알고리즘 = 정점 선택을 기반으로 하는 알고리즘, 이전 단계에서 만들어진 신장 트리를 확장하는 방법
<알고리즘 10.7.2.1> Prim의 최소 비용 신장 트리 알고리즘 #1
// 최소 비용 신장 트리를 구하는 Prim의 알고리즘
// 입력: 네트워크 G=(V,E), S는 시작 정점
// 출력: Vt, 최소 비용 신장 트리를 이루는 정점들의 집합
Prim(G,s)
Vt <- {s}: vcounter <- 1
while vcounter < n do
(u,v)는 u∈Vt and v∉Vt인 최저 비용 간선;
if (그러한 (u,v)가 존재하면)
then Vt <- Vt U v; vcounter <- vcounter +1
else 실패
return Vtprim 알고리즘의 구현
- dist라는 정점의 개수 크기의 배열이 필요함, 현재까지 알려진 신장 트리 정점 집합에서 각 정점까지의 거리를 가지고 있음.
- 처음에는 시작 노드만 값이 0이고 다른 노드는 전부 무한대 값을 가짐
- 정점들이 트리 집합에 추가되면서 dis 값은 변경됨
- 우선순위 큐 Q가 하나 필요함, 우선순위 큐 Q에 모든 정점을 삽입, 이때 우선순위는 dist 배열 값이 됨
- while 루프로 Q에서 가장 작은 dist 값을 가지는 정점을 추출
- 추출된 정점이 트리 집합에 추가됨
- 트리 집합에 새로운 정점 u가 추가되었으므로 u에 인접한 정점 v들의 dist 값들을 변경시켜줌 -> 기존의 dist[v]값 보다 간선 (u,v)의 가중치가 적으면 간선 (u,v)의 가중치로 dist[v]를 변경시킴
- Q에 있는 모든 정점들이 소진될 때까지 이러한 과정을 되풀이하면 됨
<알고리즘 10.7.2.2> Prim의 최소 비용 신장 트리 알고리즘 #2
// 최소 신장 트리를 구하는 Prim의 알고리즘
// 입력: 네트워크 G=(V,E), s는 시작 정점
// 출력: 최소 비용 신장 트리를 이루는 정점들의 집합
Prim(G, s)
for each u ∈ V do
dist[u] <- ∞
dist[s] <- 0
우선순위 큐Q에 모든 정점을 삽입(우선순위는 dist[])
for i <- 0 to n-1 do
u <- delete_min(Q)
화면에 u 출력
for each v ∈ (u의 인접 정점)
if(v ∈ Q and weight[u][v] < dist[v])
then dist[v] <- weight[u][v]<프로그램 10.7.2.1> Prim의 최소 비용 신장 트리 프로그램
#include <stdio.h>
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 7
#define INF 1000L
int weight[MAX_VERTICES][MAX_VERTICES] = {
{ 0, 29, INF, INF, INF, 10, INF },
{ 29, 0, 16, INF, INF, INF, 15 },
{ INF, 16, 0, 12, INF, INF, INF },
{ INF, INF, 12, 0, 22, INF, 18 },
{ INF, INF, INF, 22, 0, 27, 25 },
{ 10, INF, INF, INF, 27, 0, INF },
{ INF, 15, INF, 18, 25, INF, 0 }
};
int selected[MAX_VERTICES];
int dist[MAX_VERTICES];
// 최소 dist[v]값을 갖는 정점을 반환
int get_min_vertex(int n){
int v;
for (int i = 0; i < n;i++){
if(!selected[i]){
v = i;
break;
}
}
for (int i = 0; i < n;i++){
if(!selected[i] &&(dist[i] < dist[v]))
v = i;
}
return v;
}
void prim(int s, int n){
int i, u, v;
// 초기화
for (u = 0; u < n;u++){
dist[u] = INF;
selected[u] = FALSE;
}
dist[s] = 0;
for (i = 0; i < n;i++){
u = get_min_vertex(n);
selected[u] = TRUE;
if(dist[u] == INF)
return;
printf("%d ", u);
for (v = 0; v < n;v++){
if(weight[u][v] != INF){
if(!selected[v] && weight[u][v] < dist[v]){
dist[v] = weight[u][v];
}
}
}
}
}
int main(){
prim(0, MAX_VERTICES);
}
Prim 알고리즘의 분석
- 주 반복문이 정점의 수 n만큼 반복, 내부 반복문이 n번 반복하므로 시간복잡도는
- 희박한 그래프를 대상으로할 경우 Kurskal의 알고리즘이 적합, 밀집한 그래프의 경우 Prim의 알고리즘이 적합
10.8 최단 경로
최단 경로(shortest path): 네트워크에서 정점 u와 정점 v를 연결하는 경로 중에서 간선들의 가중치 합이 최소가 되는 경로를 찾는 문제
- Dijkstra 알고리즘: 하나의 시작 정점에서 모든 다른 정점까지의 최단 경로를 구함
- Floyd 알고리즘: 모든 정점에서 다른 모든 정점까지의 최단 경로를 구함
인접 행렬: 간선이 없으면 인접 행렬의 값은 0
가중치 인접 행렬: 간선의 가중치가 0일 수도 있기 때문에 간선이 없는 경우 값은 무한대(정수 중에서 상당히 큰 값)
10.8.1 Dijkstra의 최단 경로 알고리즘
Dijkstra 알고리즘: 하나의 시작 정점에서 모든 다른 정점까지의 최단 경로를 구함
- 최단 경로: 경로의 길이순으로 구해짐
- 집합 S를 시작 정점 v로부터의 최단 경로가 이미 발견된 정점들의 집합
- Dijkstra에서는 시작 정점에서 집합 S에 있는 정점만을 거쳐서 다른 정점으로 가는 최단 거리를 기록하는 배열이 필요 -> 1차원 배열: distance
- distance의 초기값- 시작 정점 distance[v] = 0
- 다른 정점 distance[w] = weight[v][w] (시작 정점과 해당 정점 간의 가중치)
- 알고리즘은 매 단계에서 집합 S 안에 있지 않은 정점 중에서 가장 distance 값이 작은 정점을 집합 S에 추가
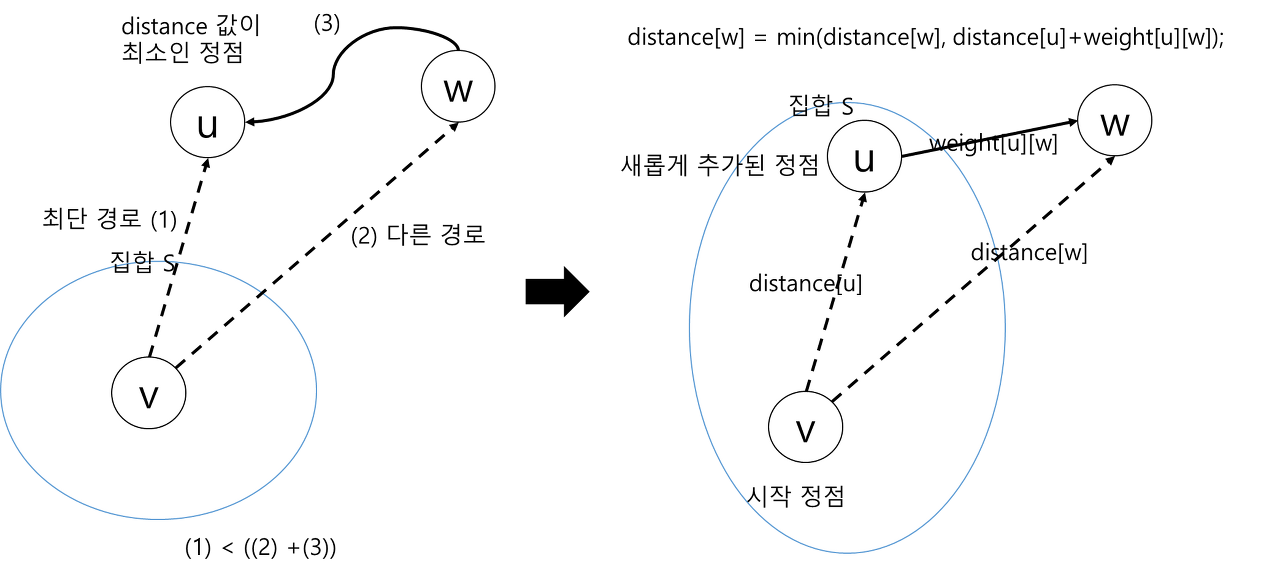
- 현재 집합 S에 들어 있지 않은 정점 중 distance 값이 가장 작은 정점이 u일 때, 시작 정점 v에서 정점 u까지의 최단 거리는 경로 (1)이 됨
- 정점 w를 거쳐서 정점 u로 가는 가상적은 더 짧은 경로가 있을 경우, 정점 v에서 정점 u까지의 최단 거리는 정점 v에서 정점 w까지의 거리 (2)와 정점 w에서 정점 u로 가는 거리 (3)을 합한 값이 됨
-> 하지만, 현재 distance 값이 가장 작은 정점은 u이기 때문에 경로 (2)는 경로 (1)보다 항상 길 수밖에 없음 - 새로운 정점 u가 집합 S에 추가되면, S에 있지 않은 다른 정점들의 distance 값을 수정
distance[w] = min(distance[w], distance[u] + weight[u][w]) // 새로 추가된 정점 u를 거쳐서 정점까지 가는 거리와 기존 거리를 비교해서 더 작은 거리로 distance 값을 수정
<알고리즘 10.8.1.1> 최단 경로 알고리즘
// 입력: 가중치 그래프 G, 가중치는 음수가 아님
// 출력: distance 배열, distance[u]는 v에서 u까지의 최단 거리
shortest_path(G, v)
S <- {v}
for 각 정점 w ∈ G do
distance[w] <- weight[u][w];
while 모든 정점이 S에 포함되지 않으면 do
u <- 집합 S에 속하지 않는 정점 중에서 최소 distance 정점;
S <- S U {u}
for u에 인접하고 S에 있지 않은 각 정점 w do
if distanace[u] + weight[u][w] < distance[w]
then distance[w] <- distance[u] + weight[u][w];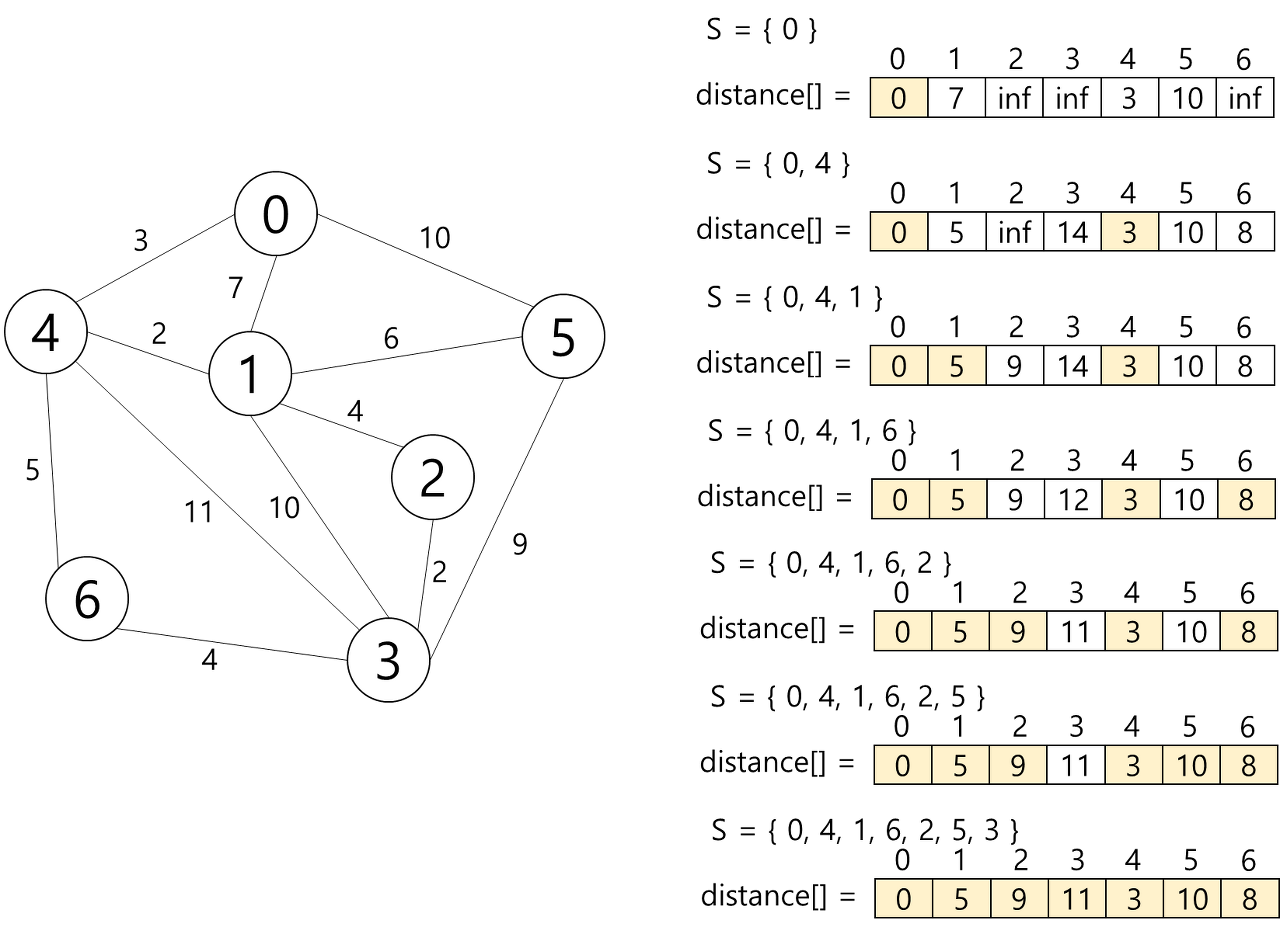
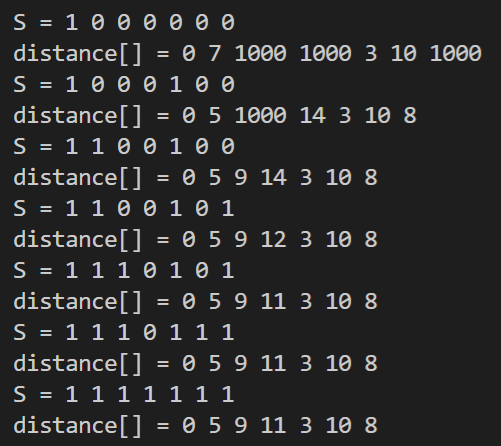
<프로그램 10.8.1.1> 최단 경로 Dijkstra 프로그램
#include <stdio.h>
#define INT_MAX 2147483647 // 최대 정수
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 7 // 정점의 수
#define INF 1000 // 무한대(연결이 없는 경우)
int weight[MAX_VERTICES][MAX_VERTICES] = { // 네트워크 인접 행렬
{ 0, 7, INF, INF, 3, 10, INF },
{ 7, 0, 4, 10, 2, 6, INF },
{ INF, 4, 0, 2, INF, INF, INF },
{ INF, 10, 2, 0, 11, 9, 4 },
{ 3, 2, INF, 11, 0, INF, 5 },
{ 10, 6, INF, 9, INF, 0, INF },
{ INF, INF, INF, 4, 5, INF, 0 }
};
int distance[MAX_VERTICES]; // 시작 정점으로부터의 최단 경로 거리
int found[MAX_VERTICES]; // 방문한 정점 표시
void print(int n)
{
printf("S = ");
for (int i = 0; i < n; i++) {
printf("%d ", found[i]);
}
printf("\n");
printf("distance[] = ");
for (int i = 0; i < n; i++) {
printf("%d ", distance[i]);
}
printf("\n");
}
int choose(int distance[], int n, int found[]){ // 최소값을 선택
int min = INT_MAX;
int minpos = -1;
for (int i = 0; i < n;i++){
if(distance[i] < min && !found[i]){
min = distance[i];
minpos = i;
}
}
return minpos;
}
void shortest_path(int start, int n){
// 초기화
for (int i = 0; i < n;i++){
distance[i] = weight[start][i];
found[i] = FALSE;
}
found[start] = TRUE; // 시작 정점 방문 표시
distance[start] = 0;
print(n);
for (int i = 0; i < n - 1;i++){
int u = choose(distance, n, found);
found[u] = TRUE;
for (int w = 0; w < n;w++){
if(!found[w]){
if(distance[u] + weight[u][w] < distance[w]){
distance[w] = distance[u] + weight[u][w];
}
}
}
print(n);
}
}
int main(){
shortest_path(0, MAX_VERTICES);
}
시간복잡도
- 주 반복문 n번 반복, 내부 반복문을 2n번 반복하므로 의 복잡도를 가짐
10.8.2 Floyd의 최단 경로 알고리즘
인접행렬 weight
1. i == j, weight[i][j] =0
2. 정점 i, j 사이 간선이 존재하지 않으면, weight[i][j] = 무한대
3. 정점 i, j 사이 간선이 존재하면, weight[i][j] = 간선(i, j)의 가중치
<알고리즘 10.8.2.1> Floyd의 최단 경로 알고리즘
floyd(G)
for k <- 0 to n-1
for i <- 0 to n-1
for j <- 0 to n-1
A[i][j] <- min(A[i][j], A[i][k]+A[k][j])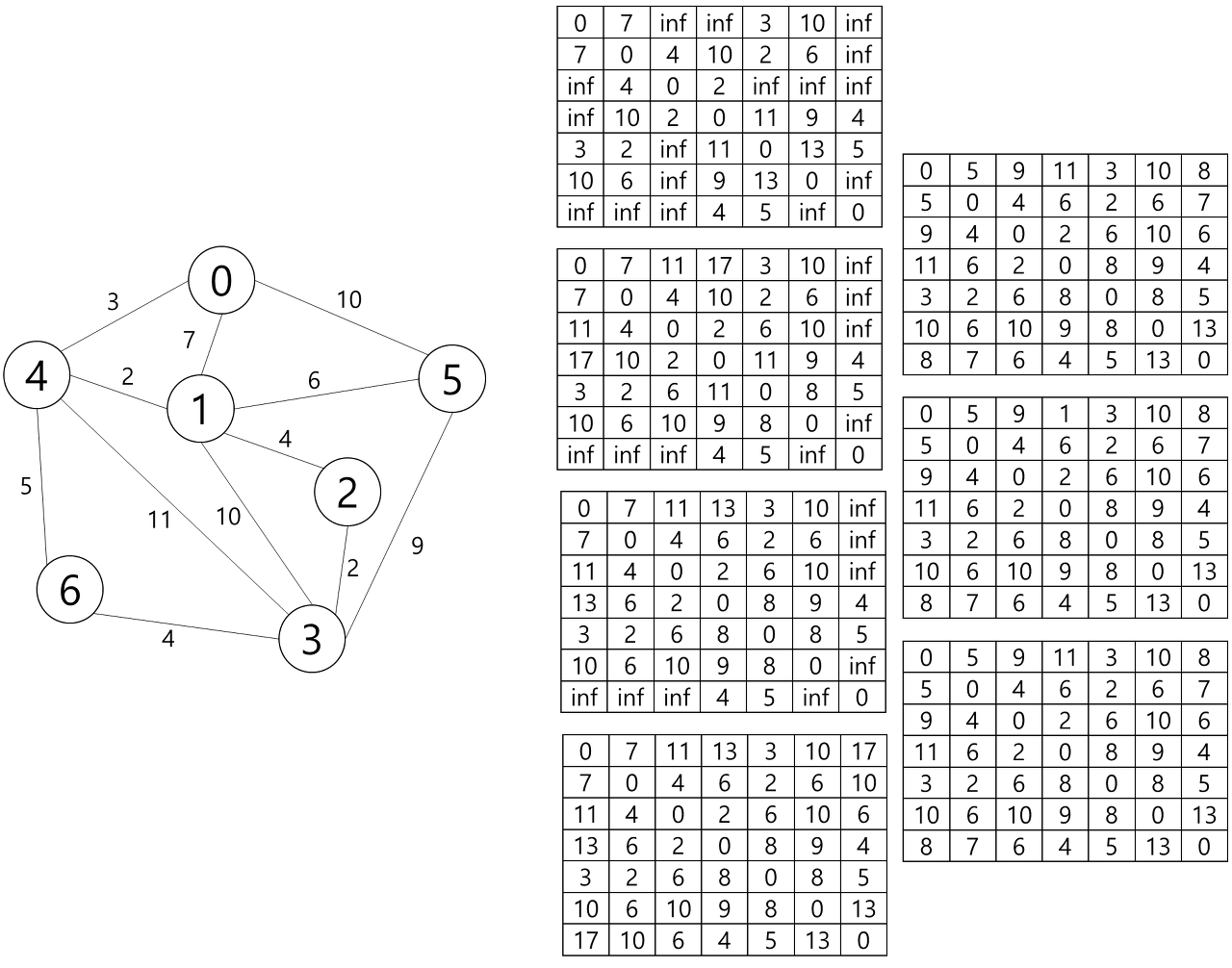
<프로그램 10.8.2.1> Floyd의 최단 경로 알고리즘
#include <stdio.h>
#define min(x,y) (((x) < (y)) ? (x):(y))
#define MAX_VERTICES 7 // 정점의 수
#define INF 1000 // 무한대(연결이 없는 경우)
int weight[MAX_VERTICES][MAX_VERTICES] = { // 네트워크 인접 행렬
{ 0, 7, INF, INF, 3, 10, INF },
{ 7, 0, 4, 10, 2, 6, INF },
{ INF, 4, 0, 2, INF, INF, INF },
{ INF, 10, 2, 0, 11, 9, 4 },
{ 3, 2, INF, 11, 0, INF, 5 },
{ 10, 6, INF, 9, INF, 0, INF },
{ INF, INF, INF, 4, 5, INF, 0 }
};
int A[MAX_VERTICES][MAX_VERTICES];
void print(int n){
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
printf("%4d ", A[i][j]);
}
printf("\n");
}
printf("\n");
}
void floyd(int n){
for (int i = 0; i < n;i++){
for (int j = 0; j < n;j++){
A[i][j] = weight[i][j];
}
}
for (int k = 0; k < n;k++){
for (int i = 0; i < n;i++){
for (int j = 0; j < n;j++){
A[i][j] = min(A[i][j], A[i][k] + A[k][j]);
}
}
print(n);
}
}
int main(){
floyd(MAX_VERTICES);
}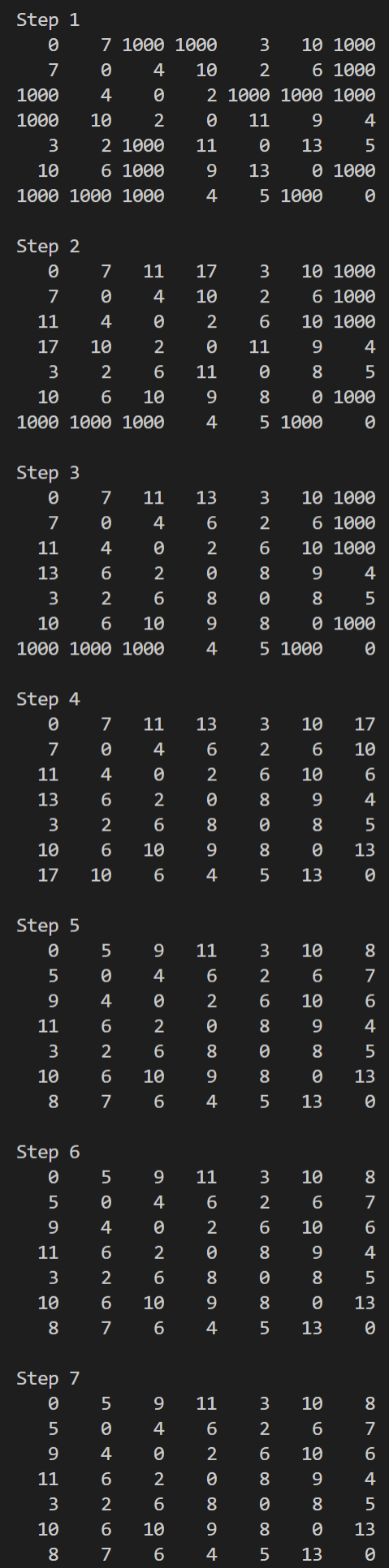
시간복잡도
- 두 개의 정점 사이의 최단 경로를 찾는 Dijkstra의 알고리즘은 시간복잡도가 이므로, 모든 정점 쌍의 최단 경로를 구하려면 n번 반복해야하기 때문에 시간복잡도가 이됨
- 한 번에 모든 정점 간의 최단 경로를 구하는 Floyd의 알고리즘은 3중 반복문 실행으로 시간복잡도 이 됨
-> Dijkstra의 알고리즘과 비교해도 차이가 없다고 할 수 있지만, Floyd 알고리즘은 매우 간결한 반복 구문을 사용하므로 Dijkstra의 알고리즘보다 상당히 빨리 모든 정점 간의 최단 경로를 찾을 수 있음
크루스칼(Kruskal)다익스트라(Dijkstra)
| 구현 방법 | 우선순위 큐 + union-find(서로소집합) | 우선순위 큐+ dp(점화식) |
| 중심 | 간선 | 정점 |
| 시작점 | 간선의 가중치가 작은 것부터 시작(오름차순 정렬) | 출발점이 정해져 있는 경우 |
| Queue 진입 시점 | 모든 정점을 유선순위 큐에 넣고 시작 | dp 갱신될 때만(최단 경로 갱신) 그 정점에서 출발하는 간선을 우선순위 큐에 추가 |
| 용도 | 최소 신장 트리를 그릴 때 | 한 정점에서 다른 정점의 최단 거리를 구하는 경우 |
| 최단 거리 | 최소의 비용(최단 거리) 모든 점을 다 연결할 때 사용 모든 점을 다 이은 경로가 최단 거리라고 말할 수 있지만 임의의 두 점 간의 거리가 최단 거리라는 보장은 없음 |
임의의 두 점 간의 최단 거리 구할 때 사용 |
10.9 위상 정렬
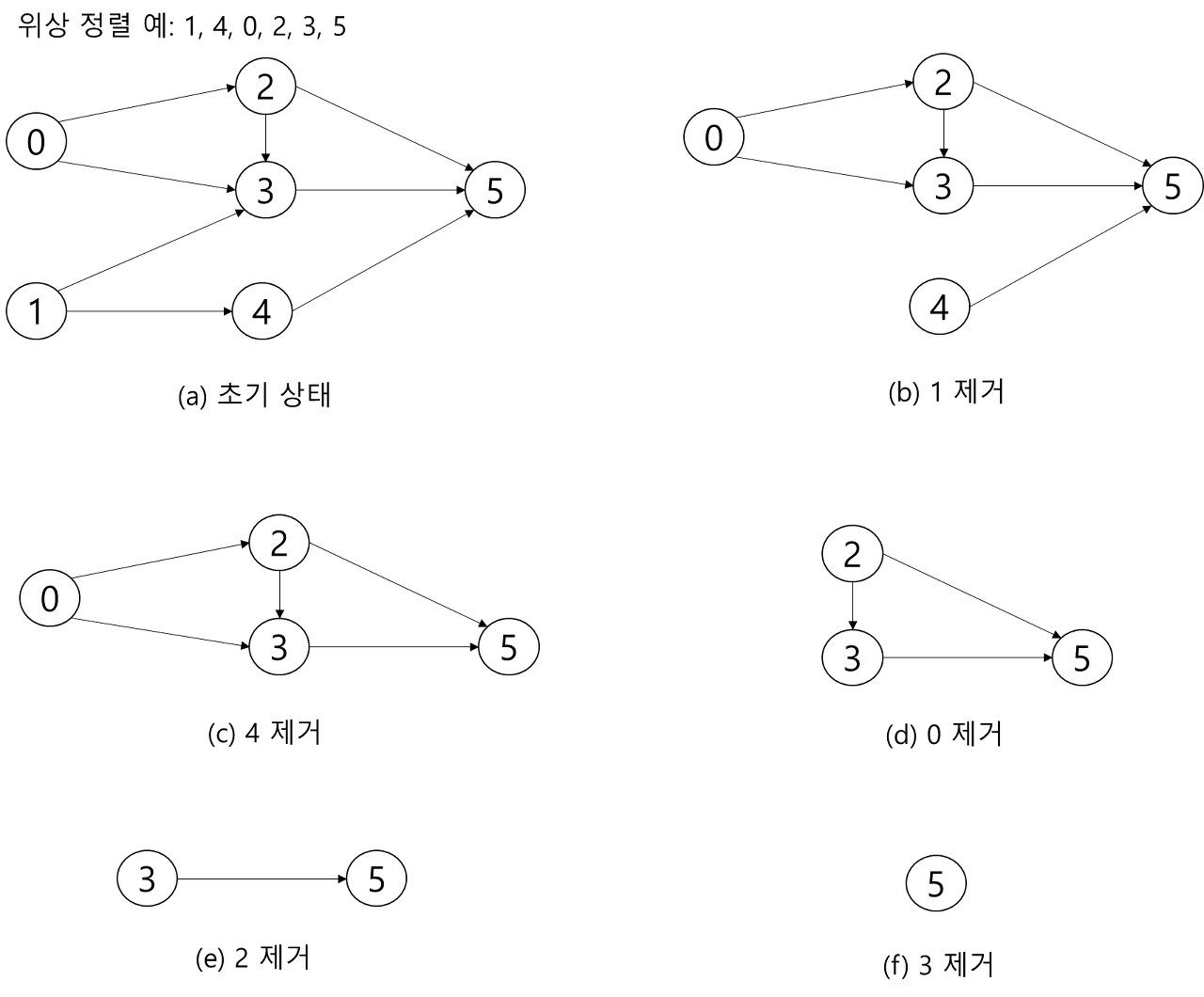
위상 정렬(topological sort): 방향 그래프에 존재하는 각 정점들의 선행 순서를 위배하지 않으면서 모든 정점을 나열하는 것
1. 진입 차수가 0인 정점을 선택
-> 진입 차수 0인 정점이 여러 개 존재할 경우 어느 정점을 선택해도 무방함(하나의 그래프에는 복수의 위산 순서가 있을 수 있음)
2. 선택된 정점과 여기에 부속된 모든 간선 삭제
3. 1,2을 반복하다가 모든 정점이 선택 및 삭제되면 종료
-> 이 과정에서 선택되는 정점의 순서를 위상 순서(topological order)라고 함
<알고리즘 10.9.1> 그래프 위상 정렬 알고리즘
// input: 그래프 G=(V,E)
// output: 위상 정렬 순서
topo_sort(G)
for i <- 0 to n-1 do
if( 모든 정점이 선행 정점을 가지면 )
then 사이클이 존재하고 위상 정렬 불가;
선행 정점을 가지지 않는 정점 v를 선택;
v를 출력;
v와 v에 부속한 모든 간선들을 그래프에서 삭제;- in_degree라는 1차원 배열을 만들어 각 정점의 진입 차수를 기록
-> in_degree[i]: 정점 i로 들어오는 간선들의 개수
-> in_degree[i] == 0일 경우 i는 후보 정점 - 알고리즘이 진행되면서, 진입 차수가 0인 정점이 그래프에서 제거되면 그 정점에 인접한 정점의 in_degree는 1만큼 감소
- 후보 정점들은 스택에 저장
<프로그램 10.9.1> 그래프 위상 정렬 프로그램
// 위상 정렬을 수행함
void topo_sort(GraphType *g){
StackType s;
GraphNode *node;
// 모든 정점의 진입 차수를 계산
int *in_degree = (int *)malloc(g->n* sizeof(int));
for(int i=0;i<g->n;i++){ // 초기화
in_degree[i] = 0;
}
for(int i=0;i<g->n;i++){
node = g->adj_list[[i]; // 정점 i에서 나오는 간선들
while(node != NULL){
in_degree[node->vertex]++;
node = node->link;
}
}
// 진입 차수가 0인 정점(후보 정점)을 스택에 삽입
init(&s)
for(int i=0;i<g->n;i++){
if(in_degree[i] == 0) push(&s, i);
}
// 위상 순서 생성
while(!is_empty(&S)){
int w;
w = pop(&s);
printf("%d ", w); // 정점 출력
node = g->adj_list[w]; // 각 정점의 진입 차수 변경
while(node != NULL){
int u = node->vertex;
in_degree[u]--; // 진입 차수 감소
if(in_degree[u] == 0){
push(&s,u);
}
node = node->link; // 다음 정점
}
}
free(in_degree);
return; // 반환 값이 1이면 성공, 0이면 실패
}<프로그램 10.9.2> 그래프 위상 정렬 전체 프로그램
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 50
typedef struct GraphNode{
int vertex;
struct GraphNode* link;
} GraphNode;
typedef struct{
int n; // wjdwjadml rotn
GraphNode* adj_list[MAX_VERTICES];
} GraphType;
// 그래프 초기화
void graph_init(GraphType *g){
g->n = 0;
for (int i = 0; i < MAX_VERTICES;i++){
g->adj_list[i] = NULL;
}
}
// 정점 삽입 연산
void insert_vertex(GraphType *g, int v){
if((g->n+1) >MAX_VERTICES){
fprintf(stderr, "graph: Exceeding the number of vertices\n");
return;
}
g->n++;
}
// 간선 삽입 연산, v를 u의 인접 리스트에 삽입
void insert_edge(GraphType*g, int u, int v){
GraphNode* node;
if(u >=g->n || v>=g->n){
fprintf(stderr, "graph: Number error at vertex\n");
return;
}
node = (GraphNode*)malloc(sizeof(GraphNode));
node->vertex = v;
node->link = g->adj_list[u];
g->adj_list[u] = node;
}
// 스택 소스 추가
#define MAX_STACK_SIZE 100
typedef int element;
typedef struct {
element stack[MAX_STACK_SIZE];
int top;
} StackType;
// 스택 초기화 함수
void init(StackType *s){
s->top = -1;
}
// 공백 상태 검출 함수
int is_empty(StackType *s){
return (s->top == -1);
}
// 포화 상태 검출 함수
int is_full(StackType *s){
return (s->top == (MAX_STACK_SIZE-1));
}
// 삽입 함수
void push(StackType *s, element data){
if(is_full(s)){
fprintf(stderr, "overflow\n");
exit(1);
}else{
s->stack[++(s->top)] = data;
}
}
// 삭제 함수
element pop(StackType *s){
if(is_empty(s)){
fprintf(stderr, "underflow\n");
exit(1);
}else{
return s->stack[(s->top)--];
}
}
// 피크 함수
element peek(StackType* s)
{
if (is_empty(s)) {
fprintf(stderr, "underflow\n");
exit(1);
} else {
return s->stack[s->top];
}
}
// 위상 정렬을 수행함
void topo_sort(GraphType* g)
{
StackType s;
GraphNode* node;
// 모든 정점의 진입 차수를 계산
int* in_degree = (int*)malloc(g->n * sizeof(int));
for (int i = 0; i < g->n; i++) { // 초기화
in_degree[i] = 0;
}
for (int i = 0; i < g->n; i++) {
node = g->adj_list[i]; // 정점 i에서 나오는 간선들
while(node != NULL){
in_degree[node->vertex]++;
node = node->link;
}
}
// 진입 차수가 0인 정점을 스택에 삽입
init(&s);
for (int i = 0; i < g->n; i++) {
if (in_degree[i] == 0)
push(&s, i);
}
// 위상 순서 생성
while (!is_empty(&s)) {
int w;
w = pop(&s);
printf("%d ", w); // 정점 출력
node = g->adj_list[w]; // 각 정점의 진입 차수 변경
while (node != NULL) {
int u = node->vertex;
in_degree[u]--; // 진입 차수 감소
if (in_degree[u] == 0) {
push(&s, u);
}
node = node->link; // 다음 정점
}
}
free(in_degree);
return; // 반환 값이 1이면 성공, 0이면 실패
}
int main(){
GraphType g;
graph_init(&g);
insert_vertex(&g, 0);
insert_vertex(&g, 1);
insert_vertex(&g, 2);
insert_vertex(&g, 3);
insert_vertex(&g, 4);
insert_vertex(&g, 5);
// 정점 0의 인접 리스트 생성
insert_edge(&g, 0, 2);
insert_edge(&g, 0, 3);
// 정점 1의 인접 리스트 생성
insert_edge(&g, 1, 3);
insert_edge(&g, 1, 4);
// 정점 21의 인접 리스트 생성
insert_edge(&g, 2, 3);
insert_edge(&g, 2, 5);
// 정점 3의 인접 리스트 생성
insert_edge(&g, 3, 5);
// 정점 4의 인접 리스트 생성
insert_edge(&g, 4, 5);
// 위상 정렬
topo_sort(&g);
// 간선을 삭제하는 함수 추가
}
'다양한 글들 > 자료구조와 알고리즘' 카테고리의 다른 글
| 자료구조 기말정리 (0) | 2023.06.15 |
|---|---|
| 자료구조 대학 강의 정리 (0) | 2023.05.15 |
| 그래프 I (0) | 2023.05.14 |
| 힙 (1) | 2023.05.14 |
| 우선순위 큐 (0) | 2023.05.14 |
