Reference :
건국대학교 컴퓨터공학과 자료구조 수업 / 김성열 교수님
C언어로 쉽게 풀어쓴 자료구조 / 천인국 / 생능출판사
선택 정렬의 원리
선택 정렬은 가장 이해하기 쉬운 정렬 방법이다
숫자들은 1차원 배열에 들어 있다고 가정
왼쪽 리스트 : 정렬이 완료된 숫자들
오른쪽 리스트 : 정렬되지 않은 숫자들
선택 정렬
: 오른쪽 리스트에서 가장 작은 숫자를 선택하여 왼쪽 리스트로 이동하는 작업을 되풀이 해서 오른쪽 리스트가 공백 상태가 될 때까지 이 과정을 되풀이하는 정렬 기법

위의 방법은 배열로 구현하기로 하였다면, 위의 방법을 구현하기 위해서는 입력 배열과는 별도로 똑같은 크기의 배열이 하나 더 필요하다.
==> 따라서 메모리를 절약하기 위하여 입력 배열 외에 추가적인 공간을 사용하지 않는 선택 정렬 알고리즘을 생각해보면 입력 배열 이외에는 다른 추가 메모리를 요구하지 않는 정렬 방법을 제자리 정렬(in-place-sorting)이라고 한다
*오른쪽 리스트에 하나의 최솟값이 선택되고 그 값이 왼쪽 배열로 이동되면 하나의 빈공간이 생기는 것을 이용한다*

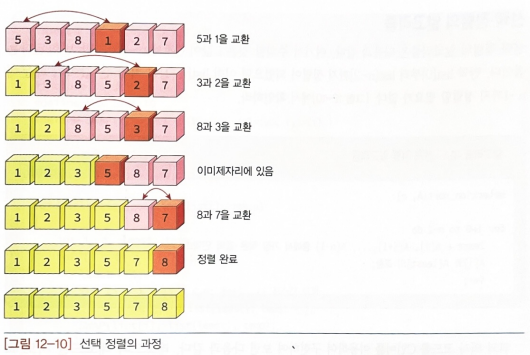
선택 정렬의 과정
- 입력 배열에서 최솟값을 발견
- 이 최솟값을 배열의 첫 번째 요소와 교환
- 첫 번째 요소를 제외한 나머지 요소들 중에서 가장 작은 값을 선택하고 이를 두 번째 요소와 교환
- 이 절차를 (숫자 개수-1)만큼 되풀이하면 추가적인 배열을 사용하지 않고서도 전체 숫자들이 정렬
선택 정렬의 알고리즘
i 값이 0 에서 n - 2 까지만 변화된다는 점이다
만약 list[0]부터 list[n-2]까지 정렬이 되었으면 이미 list[n-1]이 가장 큰 값이기 때문에 n-1까지 정렬할 필요가 없다.
선택 정렬 알고리즘
selection sort(A, n)
for i <- 0 to n - 2 do
least <- A[i], A[i + 1], ...., A[n - 1] 중에서 가장 작은 값의 인덱스;
A[i]와 A[least]의 교환;
i++;
요소의 개수가 n이면 최솟값을 갖고 교환하는 과정은 n-1번만 반복하면 된다
선택 정렬 함수
#define SWAP(x, y, t) ((t)=(x), (x)=(y), (y)=(t) )
void selection_sort(int list[], int n)
{
int i, j, least, temp;
for (i = 0; i < n - 1; i++) {
least = i;
for (j = i + 1; j < n; j++)
if (list[j] < list[least]) least = j;
SWAP(list[i], list[least], temp);
}
}
전체 프로그램
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX_SIZE 10
#define SWAP(x, y, t) ((t)=(x), (x)=(y), (y)=(t))
int list[MAX_SIZE];
int n;
void selection_sort(int list[], int n)
{
int i, j, least, temp;
for (i = 0; i < n - 1; i++) {
least = i;
for (j = i + 1; j < n; j++) // 최솟값 탐색
if (list[j] < list[least]) least = j;
SWAP(list[i], list[least], temp); // 최솟값을 찾아서 배열의 첫 번째 원소와 교환
}
}
int main()
{
int i;
n = MAX_SIZE;
srand(time(NULL)); // 난수 생성기 초기화
for (i = 0; i < n; i++) // 난수 생성 및 출력
list[i] = rand() % 100; // 난수 발생 범위 0~99
selection_sort(list, n); // 선택정렬 호출
for (i = 0; i < n; i++)
printf("%d ", list[i]); // 정렬된 배열 출력
printf("\n");
return 0;
}==> 무작위로 생성된 배열이 선택 정렬에 의해서 정렬된다
선택 정렬의 분석
비교 횟수와 이동 횟수를 분석
비교 횟수를 구하기 위하여 두개의 for 루프의 실행 횟수를 계산
외부 루프 : n-1번
내부 루프 : (n - 1) - i번 ==> 0에서 n-2까지 변하는 i에 대하여 (n - 1) - i번 반복
(n-1) +(n-2) + .... +1 = n(n-1) / 2 = O(n^2)
==> 최고차 항을 제외한 나머지 모든 항과 모든 계수를 제거하므로 O(n^2)
레코드 교환 횟수 = 외부 루프의 실행 횟수
= 3번의 이동이 필요하므로 전체 이동 횟수는 3(n-1)이 된다
선택 정렬의 장점
자료 이동 횟수가 미리 결정됨
선택 정렬의 단점
이동 횟수가 3(n-1)으로 상당히 큰 편이다
또한 자료가 정렬된 경우에는 불필요하게 자기 자신과의 이동을 하게 된다
if( i != least) // 최솟값이 자기 자신이면 자료이동을 하지 않는다
SWAP(list[i], list[least], temp);
'다양한 글들 > 자료구조와 알고리즘' 카테고리의 다른 글
| 5. 쉘 정렬 (0) | 2023.03.23 |
|---|---|
| 4. 삽입 정렬 (Insertion Sort) (0) | 2023.03.23 |
| 2. 버블 정렬 (Bubble Sort) (0) | 2023.03.23 |
| 1. 정렬 알고리즘의 개요 (0) | 2023.03.23 |
| 1. 문자열 탐색 알고리즘의 개요 (0) | 2023.03.23 |
