깊이 우선 탐색과 너비 우선 탐색
스택을 사용하는 것 : 깊이 우선 탐색 (DFS. Depth First Search) 전략
=> 최대한 갈 수 있는데 까지 가보고 막히면 다시 다른 길을 찾는 방식
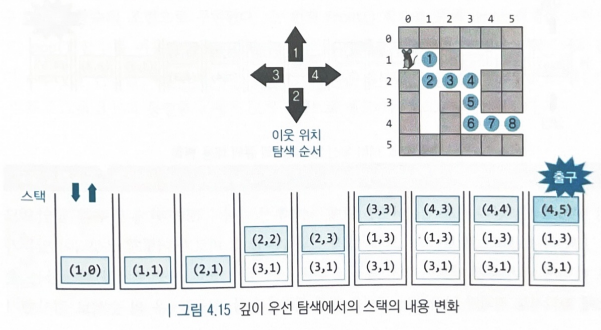
- 이웃의 탐색 순서는 그림과 같이 상-하-좌-우 순으로 진행
- 현재 위치에서 생쥐는 항상 상-하-좌-우를 검사하여 갈 수 있는 위치이면 스택에 저장
- 다음으로 스택에서 꺼내지는 것은 항상 가장 최근에 저장된 위치
- 그림은 생쥐가 깊이우선으로 탐색하는 순서를 표시하고 스택의 변화를 보여주고 있음
큐를 사용하는 것 : 너비 우선 탐색 (BFS, Breadth First Search) 전략
=> 탐색 순서에서 깊이보다는 폭을 우선으로 취함
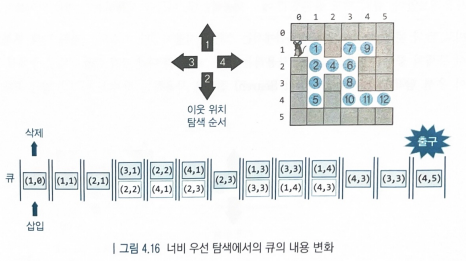
- 이 방법에서도 마찬가지로 생쥐는 현재 위치에서 상-하-좌-우 순서로 인접 위치를 검사
- 생쥐가 인접한 갈 수 있는 위치를 찾으면 저장해야 하는데, 이때 큐를 사용
- 한 위치에서의 처리가 끝나면 생쥐는 큐에서 다시 하나의 위치를 꺼내 현재 위치로 사용하는데, 이때 스택을 사용하는 경우와는 달리 가장 먼저 저장된 위치가 됨
[결론]
깊이 우선 탐색 : 8번
너비 우선 탐색 : 12번
DFS가 더 효율적 (항상 그렇지는 않음)
==> 미로가 어떻게 구성되는지, 이웃 위치를 탐색하는 순서에 따라서 달라짐
STL의 큐를 이용한 미로 탐색
Locationd2D.h
struct Location2D {
int row; // 현재 위치의 행 번호
int col; // 현재 위치의 열 번호
Location2D(int r = 0, int c = 0) { row = r; col = c; }
bool isNeighbor(Location2D& p) { // 위치 p가 자신의 이웃인지 검사하는 함수
return (row == p.row && (col == p.col - 1 || col == p.col + 1)) || (col == p.col && (row == p.row - 1 || row == p.row + 1));
//true를 반환하면 이웃
// false를 반환하면 이웃이 아니다
}
//연산자 오버로딩을 사용해서 위치p가 자신과 같은 위치인지를 검사하는 함수이다.
bool operator==(Location2D& p) { return row == p.row && col == p.col; }
};
Queue.cpp
#include "Location2D.h"
#include <queue>
using namespace std;
const int MAZE_SIZE = 6;
char map[MAZE_SIZE][MAZE_SIZE] =
{
{'1','1','1','1','1','1'},
{'e','0','1','0','0','1'},
{'1','0','0','0','1','1'},
{'1','0','1','0','1','1'},
{'1','0','1','0','0','x'},
{'1','1','1','1','1','1'},
};
bool isValidloc(int r, int c) {
if (r < 0 || c < 0 || r >= MAZE_SIZE || c >= MAZE_SIZE) {
return false;
}
else {
return map[r][c] == '0' || map[r][c] == 'x';
}
}
void main() {
queue<Location2D>locQueue;
Location2D entry(1, 0);
locQueue.push(entry);
while(locQueue.empty() == false) {
Location2D here = locQueue.front();
locQueue.pop();
int r = here.row;
int c = here.col;
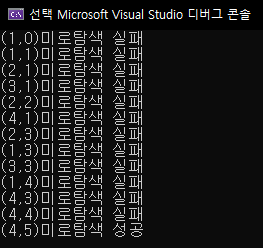
printf("(%d,%d)", r, c);
if (map[r][c] == 'x') {
printf("미로탐색 성공\n");
return;
}
else {
map[r][c] = '.';
if (isValidloc(r - 1, c)) {
locQueue.push(Location2D(r - 1, c));
}
if (isValidloc(r + 1, c)) {
locQueue.push(Location2D(r + 1, c));
}
if (isValidloc(r, c - 1)) {
locQueue.push(Location2D(r, c - 1));
}
if (isValidloc(r, c + 1)) {
locQueue.push(Location2D(r, c + 1));
}
}
printf("미로탐색 실패\n");
}
}
STL의 덱을 이용한 DFS 탐색
STL의 덱을 이용한 BFS 탐색
'자료구조와 알고리즘 ft. 수업 > 알고리즘 정리' 카테고리의 다른 글
| 8. 연결 리스트로 구현한 큐 (0) | 2023.04.20 |
|---|---|
| 7. 연결 리스트로 구현한 스택 (0) | 2023.04.20 |
| 4. 큐의 응용 (0) | 2023.04.18 |
| Array (배열) (0) | 2023.04.09 |
| array, search, insert, delete (0) | 2023.04.07 |
