1. 배열
- 배열의 개념
- 배열(array)은 거의 모든 프로그래밍 언어에서 기본적으로 제공되는 자료형
- 배열은 기본이 되는 중요한 자료형으로서 많은 자료 구조들이 배열을 사용하여 구현
- 배열은 동일한 타입의 데이터를 한 번에 여러 개 만들 때 사용됨
배열이 지원되지 않으면
int list1, list2, list3, list4, list5, list6;
그러나 배열이 지원된다면?
int list[6];
대량의 데이터를 저장하기 위하여 여러 개의 개별 변수를 사용하는 것은 "인접한 요소를 교환하라"와 같은 연산을 할 때, 매번 다른 이름으로 접근을 해야 하므로 많은 불편이 따를 수 있다.
하지만 배열을 사용하면 "연속적인 메모리 공간"이 할당되고 인덱스 (index) 번호를 사용하여 쉽게 접근이 가능하기 때문에 반복 루프를 이용하여 여러 가지 작업을 손쉽게 할 수 있다

- 배열 ADT
객체 : <인덱스, 값> 쌍의 집합
연산 :
create(size) :: = size개의 요소를 저장할 수 있는 배열 생성
get(A, I) ::= 배열 A의 i번째 요소 반환
set(A, I, V) ::= 배열 A의 i번째 위치에 값 v 저장.
C언어에서는 배열이 기본적으로 제공되기 때문에
- 1차원 배열
C언어에서 6개의 정수를 저장할 수 있는 배열을 선언
배열은 변수 이름 끝에 [ ]을 추가하여서 선언
[ ]안의 숫자는 배열의 크기
배열 ADT는 create 연산은 아래의 문장에 대응됨
int list[6]; //create 연산에 해당된다.배열 ADT의 set과 get 연산은 어떻게 구현될까?
C언어에서 배열은 아주 많이 사용되기 때문에 전용 연산자가 존재한다.
즉 [ ] 연산자를 사용하여서 원하는 인덱스에서 값을 가져오거나 값을 저장할 수 있다
list[0] = 100; // set 연산에 해당된다
value = list[0]; // get 연산에 해당된다
C에서 배열의 인덱스는 0부터 시작한다
따라서 위와 같이 선언된 배열의 요소는 list[0], list[1], list[2], list[3], list[4], list[5]가 된다
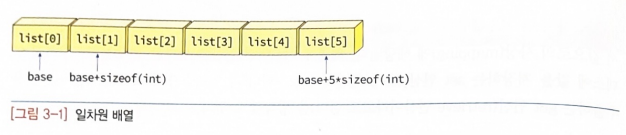
컴파일러는 배열을 어떻게 구현할까?
컴파일러는 배열에 메모리의 연속된 위치에 할당한다.
첫 번째 요소인 list[0]의 주소가 기본주소가 되고 다른 요소들의 주소는 다음과 같다

우리가 프로그램에서 list[i]라고 적으면 컴파일러는 주소 base+i*sizeof(int)에 있는 값을 가져온다
- 2차원 배열
2차원 배열은 요소들이 2차원 형태로 나열된 배열이다
2차원 배열에서 가로줄을 행(row), 세로 줄을 열 (column)이라고 한다.
C언어에서 2차원 배열은 다음과 같이 선언한다
int list[3][5];
위의 선언에서는 3개의 행과 5개의 열을 가지는 2차원 배열이 생성된다. C언어에서는 배열의 배열을 만들어서 2차원 배열을 구현한다.

- 함수의 매개변수로서의 배열
- 함수 안에서 매개 변수로 배열을 받아서 배열을 수정하면 원래의 배열이 수정됨
- 배열의 이름은 포인터와 같은 역할, 배열의 이름에 그 기반 주소가 저장되기 때문
<프로그램 3.1.1> 함수의 매개변수로서의 배열
#include <stdio.h>
#define MAX_SIZE 10
// 배열을 매개변수로 받는 함수
void sub(int var, int list[]){
var = 10;
list[0] = 10;
}
// 주 함수
int main(){
int var; // 정수 변수 선언
int list[MAX_SIZE]; // 정수 배열 선언
var = 0;
list[0] = 0;
sub(var, list);
printf("var=%d list[0]=%d\n",var,list[0]);
}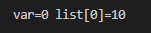
-> 프로그램 결과를 통해 sub()에서 배열 원소의 값 변경이 그 호출자인 main()에 영향을 미친다는 것을 알 수 있음.
Quiz
- C언어에서는 배열 ADT 연산들이 어떻게 구현되었는가?
- 객체: <인덱스, 요소> 쌍들의 집합
- 연산:
create(n) ::= n개의 요소를 가진 배열 생성
retrieve(A,i) ::= 배열 A의 i번째 요소 반환
store(A,i,item) ::= 배열 A의 i번째 위치에 item 저장 - int a[5][6]; 과 같이 정의된 2차원 배열에서 시작주소를 base라고 할 때 a[3][2] 요소의 주소는? -> base + 3 sizeof(int) + 2 sizeof(int);
2. 배열의 응용: 다항식
- 일반적인 다항식 형태
에서 는 계수(일반적으로 계수는 실수), 는 차수
- 첫 번째 방법
- 다항식의 모든 차수에 대한 계수 값을 배열에 저장하는 방법
ex) - 을 배열 coef에 저장, 다항식의 최고 차수는 변수 degree에 저장
- 하나의 다항식에 하나의 degree 변수와 coef 배열이 필요 -> 이를 묶어 하나의 구조체를 만들어서 다항식 표현 가능
#define MAX_DEGREE 101 // 다항식 최대 차수 + 1
typedef struct{
int degree;
float coef[MAX_DEGREE];
} polynomial;
polynomail a = {5,{10,0,0,0,6,3}};단점: 다항식의 대부분의 항의 계수가 0인 희소 다항식의 경우 공간 낭비가 심함
장점: 다항식의 덧셈이나 뺄셈 시에 같은 차수의 계수를 쉽게 찾을 수 있음
<프로그램 3.2.1> 다항식 덧셈 프로그램 #1
#include <stdio.h>
#define MAX(a,b) (((a)>(b))?(a):(b))
#define MAX_DEGREE 101
typedef struct { // 다항식 구조체 타입 선언
int degree; // 다항식의 차수
float coef[MAX_DEGREE]; // 다항식의 계수
} polynomial;
// C = A+B 여기서 A와 B는 다항식
polynomial poly_add1(polynomial A, polynomial B){
polynomial C; // 결과 다항식
int Apos = 0, Bpos = 0, Cpos = 0; // 배열 인덱스 변수
int degree_a = A.degree;
int degree_b = B.degree;
C.degree = MAX(degree_a, degree_b); // 결과 다항식의 차수
while(Apos <= A.degree && Bpos <= B.degree){
if(degree_a > degree_b){ // A항 > B항
C.coef[Cpos++] = A.coef[Apos++];
degree_a--;
} else if (degree_a == degree_b) { // A항 == B항
C.coef[Cpos++] = A.coef[Apos++] + B.coef[Bpos++];
degree_a--;
degree_b--;
} else { // A항 < B항
C.coef[Cpos++] = B.coef[Bpos++];
degree_b--;
}
}
return C;
}
// 주 함수
int main(){
polynomial a = { 5, { 3, 6, 0, 0, 0, 10 } };
polynomial b = { 4, { 7, 0, 5, 0, 1} };
polynomial c;
c = poly_add1(a, b);
printf("C's degree: %d\n", c.degree);
printf("C's coef: ");
for (int i = 0; i <= c.degree;i++){
printf("%.0f ", c.coef[i]);
}
printf("\n");
return 0;
}
- 두 번째 방법
- 공간을 절약하기 위해서 다항식에서 0이 아닌 항만을 하나의 전력 배열에 저장하는 방법
ex)
으로 표시 -> (계수, 차수)의 형식
- 지수(coef)-계수(expon) 쌍 구조체 선언하고 이 구조체의 배열(terms)을 생성, 구조체 배열로 다항식 표현 가능
#define MAX_TERMS 101
struct{
float coef;
int expon;
}terms[MAX_TERMS];장점: 구조체 배열 안에 항의 총 개수가 MAX_TERMS를 넘기지 않으면 많은 다항식을 저장할 수 있음
단점: 하나의 다항식이 시작되고 끝나는 위치를 가리키는 변수들을 관리해야 함. 차수도 저장해야하기 때문에 다항식에 따라서는 계수만을 저장하는 첫 번째 방법보다 공간이 더 많이 필요할 수도 있음.
<프로그램 3.2.2> 다항식 덧셈 프로그램 #2
#include <stdio.h>
#include <stdlib.h>
#define MAX_TERMS 101
struct {
float coef;
int expon;
} terms[MAX_TERMS] ={{8,3},{7,1},{1,0},{10,3},{3,2},{1,0}};
int avail = 6; // 현재 비어 있는 요소의 인덱스를 가리킴
// 두 개의 정수를 비교
char compare(int a, int b){
if(a>b)
return '>';
else if(a==b)
return '=';
else
return '<';
}
// 새로운 항을 다항식에 추가
void attach(float coef, int expon){ // 해당 항목들을 배열 terms의 다음 빈 공간에 더하는 함수
if(avail > MAX_TERMS){
fprintf(stderr, "Too many terms\n");
exit(1);
}
terms[avail].coef = coef;
terms[avail++].expon = expon;
}
// C = A + B
void poly_add2(int As, int Ae, int Bs, int Be, int *Cs, int *Ce){
float tmpcoef;
*Cs = avail;
while(As <= Ae && Bs <= Be){
switch (compare(terms[As].expon,terms[Bs].expon))
{
case '>': // A의 차수 > B의 차수
attach(terms[As].coef, terms[As].expon);
As++;
break;
case '=': // A의 차수 = B의 차수
tmpcoef = terms[As].coef + terms[Bs].coef;
if(tmpcoef){
attach(tmpcoef, terms[As].expon);
}
As++;
Bs++;
break;
case '<': // A의 차수 < B의 차수
attach(terms[Bs].coef, terms[Bs].expon);
Bs++;
break;
}
}
// A의 나머지 항들을 이동
for (; As <= Ae;As++){
attach(terms[As].coef, terms[As].expon);
}
// B의 나머지 항들을 이동
for (; Bs <= Be; Bs++) {
attach(terms[Bs].coef, terms[Bs].expon);
}
*Ce = avail - 1;
}
// 주 함수
int main(){
int cs, ce;
poly_add2(0, 2, 3, 5, &cs, &ce);
for (int i = cs; i <= ce;i++){
printf("(%0.f %d) ", terms[i].coef, terms[i].expon);
}
printf("\n");
return 0;
}
Quiz
- 다항식 를 첫 번째 방법으로 표현하기 -> {3, {6, 8, 0, 9}}
- 다항식 를 두 번째 방법으로 표현하기 -> {(6, 3), (8, 2), (9, 0)}
- 다항식의 뺄셈을 구현 하려면 덧셈 코드의 어떤 부분을 변경하면 되는가? A의 차수와 B의 차수가 동일한 부분의 코드를 뺄셈으로 수정하면 된다.
3. 배열의 응용: 희소 행렬
행렬(matrix) 표현 방법
- 2차원 배열 사용
#define MAX_ROWS 100
#define MAX_COLS 100
int matrix[MAX_ROWS][MAX_COLS];장점: 두 행렬 관련 여러 가지 연산이 쉬움
단점: 많은 항들이 0으로 되어 있는 희소 행렬의 경우, 2차원 배열을 사용하면 메모리 낭비가 심함.
<프로그램 3.3.1> 희소 행렬 덧셈 프로그램 #1
#include <stdio.h>
#define ROWS 3 // 행의 개수
#define COLS 3 // 열의 개수
// 희소 행렬의 덧셈 -> 두 행렬의 크기가 같아야 더할 수 있음
void sparse_matrix_add1(int A[ROWS][COLS], int B[ROWS][COLS], int C[ROWS][COLS]){ // C = A + B
for (int r = 0; r < ROWS;r++){
for (int c = 0; c < COLS;c++){
C[r][c] = A[r][c] + B[r][c];
}
}
}
// 주 함수
int main(){
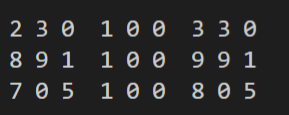
int arr1[ROWS][COLS] = { { 2, 3, 0 }, { 8, 9, 1 }, { 7, 0, 5 } };
int arr2[ROWS][COLS] = { { 1, 0, 0 }, { 1, 0, 0 }, { 1, 0, 0 } };
int arr3[ROWS][COLS];
sparse_matrix_add1(arr1, arr2, arr3);
for (int r = 0; r < ROWS;r++){
for (int c = 0; c < COLS; c++) {
printf("%d ", arr1[r][c]);
}
printf(" ");
for (int c = 0; c < COLS; c++) {
printf("%d ", arr2[r][c]);
}
printf(" ");
for (int c = 0; c < COLS;c++){
printf("%d ", arr3[r][c]);
}
printf("\n");
}
return 0;
}
- 0이 아닌 요소들만 (행, 열, 값)으로 표시하는 방법
장점: 메모리 낭비가 줄어듬
단점: 두 행렬 관련 여러 가지 연산이 복잡함
<프로그램 3.3.2> 희소 행렬 프로그램 #2
#include <stdio.h>
#include <stdlib.h>
#define ROWS 3 // 행의 개수
#define COLS 3 // 열의 개수
#define MAX_TERMS 10
typedef struct{ // 하나의 요소를 나타내는 구조체
int row; // 각 데이터가 저장된 요소의 번호
int col;
int value;
} element;
typedef struct{
element data[MAX_TERMS]; //1차원 구조체 배열
int rows; // 2차원 배열의 행의 개수
int cols; // 열의 개수
int terms; // 항의 개수
} SpareMatrix;
// 희소 행렬의 덧셈
SpareMatrix sparse_matrix_add2(SpareMatrix A, SpareMatrix B)
{ // C = A + B
SpareMatrix C;
int ca = 0, cb = 0, cc = 0; // 배열의 항목을 가리키는 인덱스
// 배열 A와 배열 B의 크기가 동일한지 확인
if(A.rows != B.rows || A.cols != B.cols){
fprintf(stderr, "SpareMatrix size error\n");
exit(1);
}
// 배열 A와 배열 B의 크기가 동일할 경우에만 실행되기 때문에 배열 A의 행, 열 크기를 배열 C의 행, 열 크기로 지정해줌
C.rows = A.rows;
C.cols = A.cols;
C.terms = 0; // 1차원 구조체 배열의 크기 == 항의 크기
while (ca < A.terms && cb < B.terms){
// 각 항목의 순차적인 번호를 계산한다.
int ind_A = A.data[ca].row * A.cols + A.data[ca].col;
int ind_B = B.data[cb].row * B.cols + B.data[cb].col;
if(ind_A < ind_B){
// 배열 A의 항목이 앞에 있으면
C.data[cc++] = A.data[ca++];
}else if(ind_A == ind_B){
// A와 B가 같은 위치
if((A.data[ca].value + B.data[cb].value)!=0){
C.data[cc].row = A.data[ca].row;
C.data[cc].col = A.data[ca].col;
C.data[cc++].value = A.data[ca++].value + B.data[cb++].value;
}else{
ca++;
cb++;
}
}else{
// 배열 B의 항목이 앞에 있으면
C.data[cc++] = B.data[cb++];
}
}
// 배열 A나 B에 남아 있는 항들을 배열 C로 옮김
for (; ca < A.terms;){
C.data[cc++] = A.data[ca++];
}
for (; cb < B.terms;) {
C.data[cc++] = B.data[cb++];
}
C.terms = cc; // 1차원 구조체 배열의 크기 == 항의 크기
return C;
}
// 주 함수
int main(){
SpareMatrix a = { { { 1, 1, 5 }, { 2, 2, 9 } }, 3, 3, 2 };
SpareMatrix b = { { { 0, 0, 5 }, { 2, 2, 9 } }, 3, 3, 2 };
SpareMatrix c;
c = sparse_matrix_add2(a, b);
printf("A: ");
for (int i = 0; i < a.terms;i++){
printf("(%d %d %d) ", a.data[i].row, a.data[i].col, a.data[i].value);
}
printf("\n");
printf("B: ");
for (int i = 0; i < b.terms; i++) {
printf("(%d %d %d) ", b.data[i].row, b.data[i].col, b.data[i].value);
}
printf("\n");
printf("C: ");
for (int i = 0; i < c.terms; i++) {
printf("(%d %d %d) ", c.data[i].row, c.data[i].col, c.data[i].value);
}
printf("\n");
return 0;
}
Quiz
- 주어진 행렬의 전치 행렬을 구하는 연산인 transpose()를 구현해보기. 희소 행렬을 표현하는 첫 번쨰 방법으로 구현
void transpose(int A[ROWS][COLS], int transA[COLS][ROWS]){
for (int r = 0; r < ROWS;r++){
for (int c = 0; c < COLS;c++){
transA[c][r] = A[r][c];
}
}
return;
}
int main(){
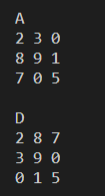
int arr1[ROWS][COLS] = { { 2, 3, 0 }, { 8, 9, 1 }, { 7, 0, 5 } };
int arr4[COLS][ROWS];
transpose(arr1, arr4);
printf("A\n");
for (int r = 0; r < ROWS; r++) {
for (int c = 0; c < COLS; c++) {
printf("%d ", arr1[r][c]);
}
printf("\n");
}
printf("\n");
printf("D\n");
for (int r = 0; r < COLS;r++){
for (int c = 0; c < ROWS;c++){
printf("%d ", arr4[r][c]);
}
printf("\n");
}
return 0;
}
'자료구조와 알고리즘 ft. 수업 > 알고리즘 정리' 카테고리의 다른 글
| 5. 덱의 응용 : 미로 탐색 프로그램 ft. C++ (0) | 2023.04.18 |
|---|---|
| 4. 큐의 응용 (0) | 2023.04.18 |
| array, search, insert, delete (0) | 2023.04.07 |
| 2. 이진 트리 (0) | 2023.03.07 |
| 1. 트리 (0) | 2023.03.07 |
