Reference :
- 컴퓨터 구조 및 설계 MIPS EDITION [6판] / David A. Patterson / 한빛에듀
- 건국대학교 컴퓨터구조 강의 / 박능수 교수님
- https://developbear.tistory.com/ (김베어의 개발일지)
레지스터
우리가 C, Java 등의 상위 수준 언어로 코딩을 했을 때에는 변수를 만들어서 그 변수에 값을 저장하면 끝이었지만,
산술 명령어의 피연산자에는 제약이 존재한다.
이들은 레지스터(register)라고 하는 하드웨어로 직접 구현된 특수 위치 몇 곳에 있는 것만을 사용할 수 있다는 것이다.
레지스터는 하드웨어 설계의 기본 요소인 동시에 프로그래머에게도 보이는 부분이므로,
컴퓨터를 구성하는 벽돌과 같다고 할 수 있다.
MIPS 구조에서는 레지스터의 크기는 32비트이다.
MIPS에서 32비트가 한 덩어리로 처리되는 일이 매우 빈번하므로 이것을 워드(word)라고 부른다.
(1 word = 32 bit = 4 byte)
프로그래밍 언어에서 사용하는 변수와 하드웨어 레지스터의 큰 차이점 하나는 레지스터는 개수가 한정되어 있다는 점이다.
레지스터의 개수는 제한되어있기 때문에
변수의 개수가 레지스터의 제한을 넘을 경우 컴파일러의 레지스터 최적화는 필수적이다.
현대 컴퓨터에서는 MIPS에서 처럼 32개의 레지스터를 갖는다.
즉, MIPS는 32비트의 레지스터를 32개 갖고 있다.
* 레지스터를 나타내기 위해 MIPS 관례는 달러 기호 뒤에 두 글자가 따라 나오는 이름을 사용한다.
1. C나 Java의 변수에 해당하는 레지스터를 위해선 $s0, $s1 등을 사용
2. MIPS 명령어로 컴파일하기 위해 필요한 임시 레지스터를 위해서는 $t0, $t1 등을 사용
(예시)
위에서 보인 C 코드 예시이다.
f = (g + h) - (i + j);
이를 레지스터를 사용해서 바꿔보면 아래와 같을 것이다.
add $t0, $s1, $s2 # register $t0 contains g + h
add $t1, $s3, $s4 # register $t1 contains i + j
sub $s0, $t0, $t1 # f gets $t0 - $t1, which is (g + h) - (i + j)
그런데 레지스터의 개수는 왜 32개로 제한했을까?
그 이유는 하드웨어 설계의 3대 원칙 중 두 번째 원칙에서 찾을 수 있다.
설계 원칙 2 : 작은 것이 더 빠르다.
레지스터가 아주 많아지면 전기 신호가 더 멀리까지 전달되어야 하므로 클럭 사이클 시간이 길어진다.
32개 이상의 레지스터를 사용하지 않는 또 다른 이유 하나는 명령어 형식에서 레지스터가 사용하는 비트 수와 관련이 있다.
(2.5절에 나올 예정)
메모리
프로그래밍 언어를 쓸 때 값 하나만 기억하는 단순한 변수 외에도 배열이나 구조체 같은 복잡한 자료구조들이 있다.
이러한 복잡한 자료구조 하나에는 레지스터 개수보다 훨씬 많은 데이터 원소가 있을 수 있는데,
이들은 컴퓨터에서 어떻게 표현되고 사용될까?
우리는 배열이나 구조체 같은 큰 자료구조는 메모리에 저장한다.
대부분의 컴퓨터는 byte 단위로 주소를 지정한다. (byte address, 1 byte = 8 bit)
워드(word) 주소를 사용할 경우 4 byte의 크기를 차지한다. (1 word = 32 bit = 4 byte)
즉, MIPS에서 word의 시작 주소는 항상 4의 배수여야 하며, 이러한 요구사항을 정렬 제약이라고 한다.
* 정렬 제약(alignment restriction) : 메모리 내에서 데이터는 자연스러운 경계를 지켜서 정렬되어야 한다는 요구 조건
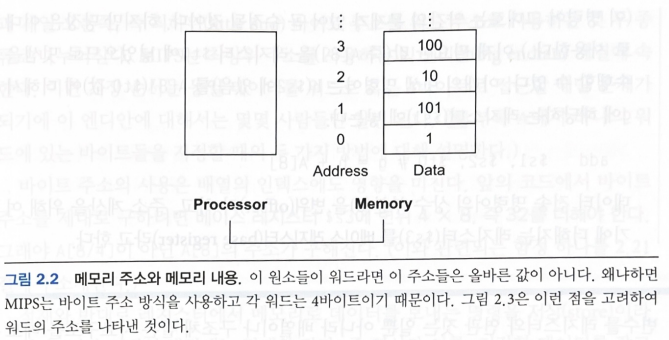
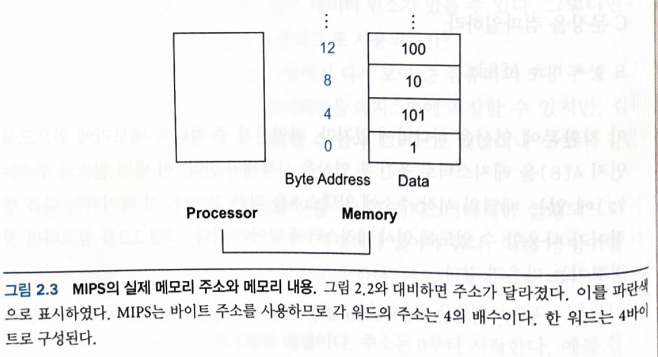
word 주소를 사용하는 방법에는 2가지가 존재한다.
1. 최상위(big end) 바이트 주소를 워드 주소로 사용 : Big-Endian
MSB(Most Significant Byte)부터 메모리에 저장하는 것이다.
2. 최하위(litte end) 바이트 주소를 워드 주소로 사용 : Little-Endian
LSB(Least Significant Byte)부터 메모리에 저장하는 것이다.
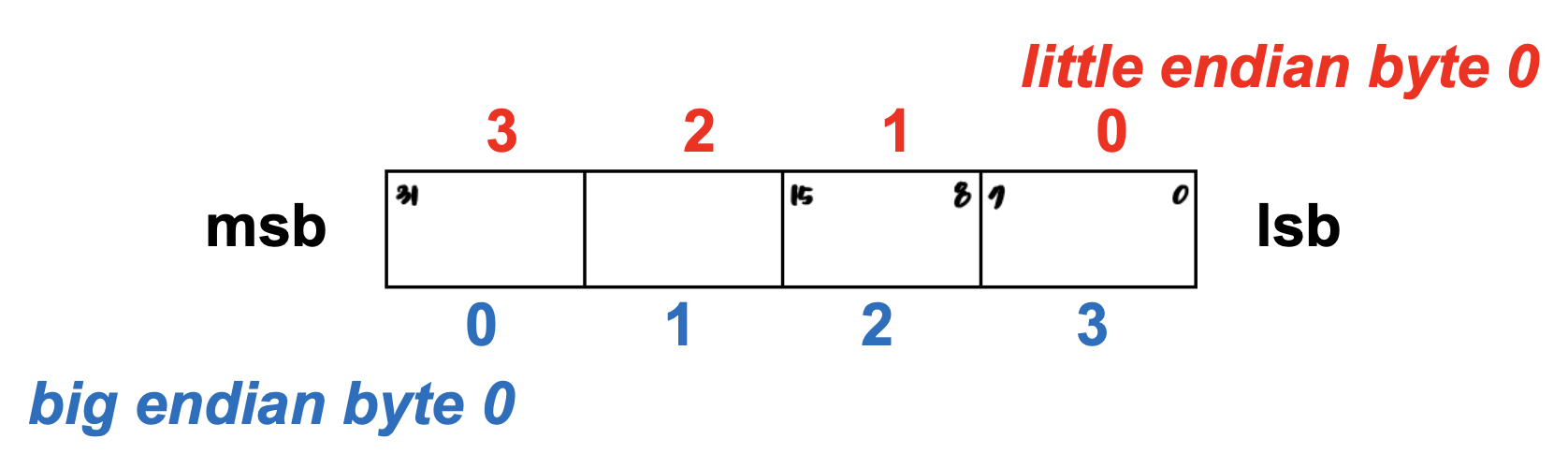
MIPS는 Big-Endian 계열에 속한다.
메모리 연산 (Memory Operands)
MIPS의 산술 연산은 레지스터에서만 실행되기 때문에 메모리와 레지스터 간에 데이터를 주고받는 명령어가 필요하다.
이때 사용되는 것이 바로 메모리 연산자이다.
- lw (load word)
메모리에서 레지스터로 데이터를 복사해 오는 데이터 전송 명령을 적재(load)라고 한다.
MIPS에서 이 명령어의 실제 이름은 lw(load word)이다.
아래의 C 코드가 있다.
g = h + A[8];g는 레지스터 $s1, h는 레지스터 $s2,
A의 시작 주소는 레지스터 $s3에 저장되어 있다고 하자. (base 레지스터 : $s3)
위의 코드를 MIPS 어셈블리 언어로 바꾸면 다음과 같다.
lw $t0, 32($s3) # Temporary reg $t0 gets A[8]
add $s1, $s2, $t0 # g = h + A[8]
A[8]은 A의 시작 주소에서 8*4(bit)=32번째 bit에 저장되어 있는 data임을 지시한다.
즉, 현재 4byte 크기의 word를 저장하고 있기 때문에
A의 시작 주소에 32가 더해져야 A[8]의 메모리 주소 상 위치로 접근할 수 있어, 32가 offset으로 곱해지는 것이다.
- sw (store word)
적재와 반대로,
레지스터에서 메모리로 데이터를 보내는 명령을 저장(store)라고 한다.
MIPS에서 이 명령어의 실제 이름은 sw(store word)이다.
아래의 C 코드가 있다.
A[12] = h + A[8];h는 레지스터 $s2, A의 시작 주소는 레지스터 $s3에 저장되어 있다고 하자.
위의 코드를 MIPS 어셈블리 언어로 바꾸면 다음과 같다.
lw $t0, 32($s3) # Temporay reg $t0 gets A[8]
add $t0, $s2, $t0 # Temporary reg $to gets h + A[8]
sw $t0, 48($s3) # Stores h + A[8] back into A[12]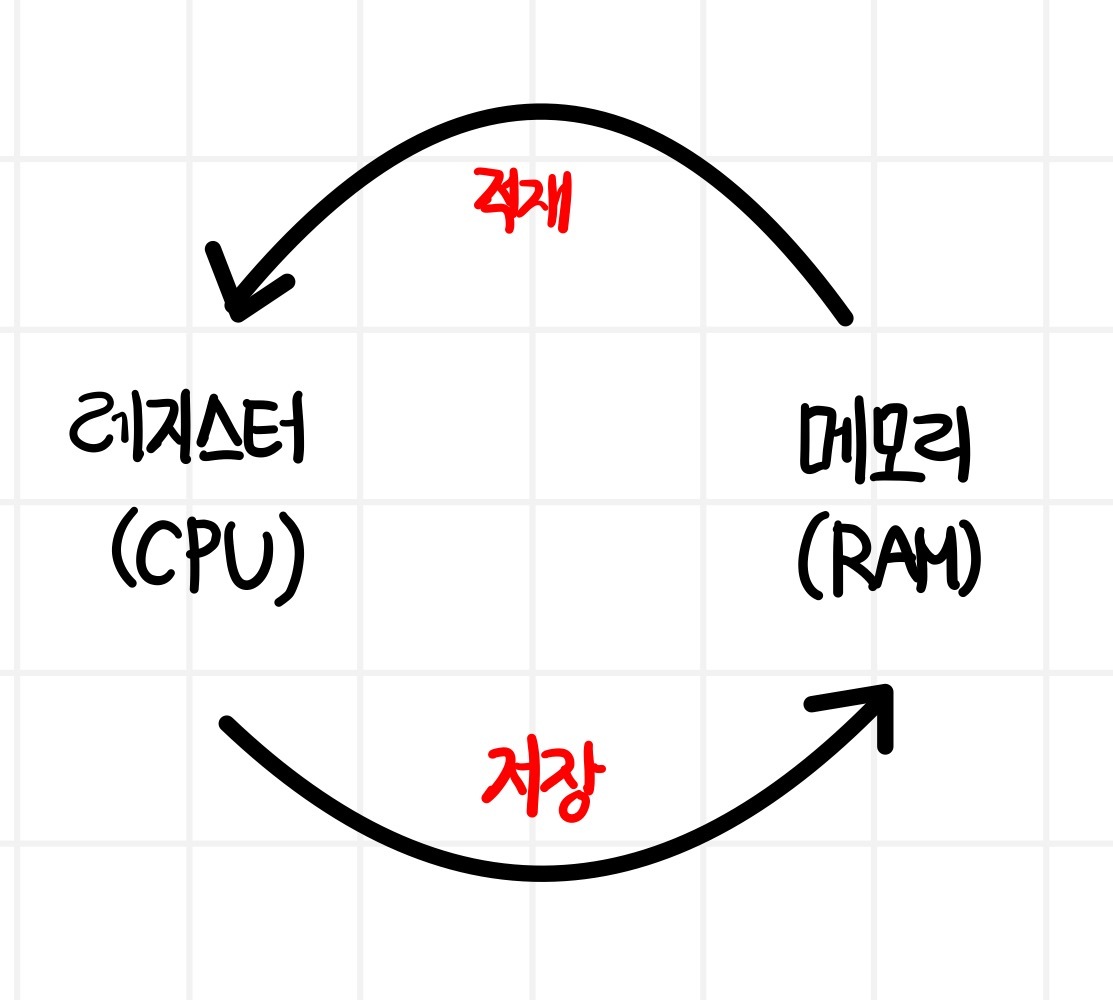
상수 연산자 (Immediate Operands)
프로그램에서 상수를 사용하는 경우는 많이 있는데, 이들은 어디에 저장하여 사용하는 것일까?
이제까지 배운 명령어만으로 상수를 사용하려면 메모리에서 상수를 읽어 와야 한다.
(상수는 프로그램이 적재될 때 메모리에 넣어짐)
예를 들어 레지스터 $s3에 상수 4를 더하는 MIPS 어셈블리 언어는 아래와 같다.
lw $t0, AddrConstant4($s1) # $t0 = constant 4
add $s3, $s3, $t0 # $s3 = $s3 + $t0 ($t0 == 4)* $s1 + AddrConstant4는 상수 4가 저장되어 있는 메모리 주소라고 가정
하지만 상수는 쓰이는 빈도가 굉장히 높은데,
그때마다 적재 명령어를 사용한다면 성능이 굉장히 좋지 않을 것이다.
따라서 하드웨어 설계의 3대 원칙 중 세 번째 원칙에 따라
피연산자 중 하나가 상수인 산술 연산 명령어를 제공하는 방법을 사용한다.
설계 원칙 3 : 자주 생기는 일을 빠르게 하라.
이 상수는 수치(immediate) 피연산자라고 하며, 수치 피연산자를 갖는 덧셈 명령어는 addi이다.
위의 예시, 레지스터 $s3에 상수 4를 더하는 MIPS 어셈블리 언어는 아래와 같다.
addi $s3, $s3, 4 # $s3 = $s3 + 4
상수 피연산자는 자주 사용되므로, 상수 필드를 갖는 산술 명령어를 사용하면
매번 메모리에서 상수를 가져오는 것보다 연산이 훨씬 빨라지고 에너지를 덜 소모하게 된다.
상수 0의 경우, $zero라는 레지스터에 따로 저장해 두고 사용한다.
상수 0은 여러 변형을 제공함으로써 단순한 명령어 집합을 가능케하기 때문이다.
예를 들어, 복사(move) 연산은 피연산자 중 하나가 0인 add 명령어이다.
따라서 레지스터 $zero를 값 0으로 묶어둔다면
따로 새로운 명령어를 만드는 것이 아닌, 기존 add 명령어를 사용하여 복사 연산을 구현할 수 있게 된다.
add $t2, $s1, $zero # move operation ($s1을 $t2로 옮길 수 있다)'컴퓨터 구조 > Ch2. 명령어 : 컴퓨터 언어' 카테고리의 다른 글
| 6. 논리 연산 명령어 (0) | 2023.03.28 |
|---|---|
| 5. 명령어의 컴퓨터 내부 표현 (0) | 2023.03.28 |
| 4. 부호있는 수와 부호없는 수 (0) | 2023.03.28 |
| 2. 하드웨어 연산 (0) | 2023.03.28 |
| 1. 서론 (0) | 2023.03.28 |
