Reference:
- 이것이 자료구조+알고리즘이다 with C언어 / 박상현 / 한빛미디어
- 건국대학교 컴퓨터공학과 자료구조 수업 / 김성렬 교수님
1. 탐색이란?
- 무언가를 찾는다
- 컴퓨터 세계에서의 무언가 = 데이터
- 즉, 데이터를 찾는다
순차 탐색
- 가장 간단한 탐색 알고리즘
이진 탐색
- 놀라운 성능을 보여주는 탐색 알고리즘이지만 모든 자료구조에서 사용할 수 있는 것은 아님
- 각 요소가 메모리에 순차적으로 적재되어 있어 그 주소를 바로 계산할 수 있는 배열에서나 사용이 가능
이진 탐색 트리
- 데이터의 크기가 동적으로 변경되는 경우에도 이진 탐색과 동일한 성능으로 탐색을 가능하게 하는 자료구조
레드 블랙 트리
- 이진 탐색 트리를 한층 더 개선한 것
2. 정렬되지 않은 배열에서의 탐색
- 순차 탐색 (Sequential Search) = 선형 탐색 (Linear Search)
- 처음부터 끝까지 차례대로 모든 요소를 비교하여 원하는 데이터를 찾는 탐색 알고리즘
- 어느 한쪽 방향으로만 탐색할 수 있는 알고리즘이므로 선형 탐색 (Linear Search) 이라고도 불림
- 정렬되지 않은 데이터에서 원하는 항목을 찾을 수 있는 유일한 방법
- 구현이 간단해서 버그를 만들 가능성이 적다는 장점
- 높은 성능이 필요하지 않거나 데이터의 크기가 작은 상황에서 유용하게 활용됨
- 순차 탐색은 배열이나 링크드 리스트에 쉽게 적용할 수 있는 알고리즘
배열을 이용한 순차 탐색
int search(int a[], int n, int x)
{
int i;
for (i=0; i<n; i++)
if (a[i] == x) return i; //배열 사용
return -1;
}
포인터를 이용한 순차 탐색
int search(int a[], int n, int x)
{
int i;
for (i=0; i<n; i++)
if (*(a+i) == x) return i; // 포인터 사용
return -1;
}- 개선된 순차 탐색
: 순차 탐색에서 비교 횟수를 줄이기 위해 리스트 끝을 테스트하는 비교 연산을 줄이기 위해 리스트의 끝에 찾고자 하는 키 값을 저장하고 반복문의 탈출 조건을 키 값을 찾을 때까지로 설정
<프로그램 12.2.2> 개선된 순차 탐색
int seq_search2(int key, int low, int high){
int i;
list[high+1] = key;
for(i= low; list[i] != key; i++){} // 키 값을 찾으면 종료 -> 비교 연산을 for문 안에서 안함
if(i == (high+1)) return -1; // 탐색 실패 시
else return i; // 탐색 성공 시
}- 순차 탐색의 시간 복잡도
탐색 성공 시 평균 (n+1)/2를 비교하고, 실패 시 n번 비교 -> 시간복잡도는
3. 정렬된 배열에서의 탐색
- 정렬된 배열에서의 순차 탐색
- 순차 탐색 실행 중 키 값보다 큰 항목을 만나면 배열의 마지막까지 검색하지 않아도 탐색 항목이 없음을 알 수 있음
- 찾고자 하는 항목이 배열의 마지막에 존재하는 경우 원래의 순차 탐색과 차이가 나지 않음
<프로그램 12.3.1.1> 정렬된 배열에서의 순차 탐색
// 오름차순으로 정렬된 배열 리스트의 순차 탐색
int sorted_seq_search(int key, int low, int high){
for(int i=low; i<=high;i++){
if(list[i] > key) retuern -1; // 키 값보다 큰 항목을 만났을 경우 return
if(list[i] == key) return i;
}
}탐색 성공 시 일반 순차 탐색과 동일, 실패 시 비교 횟수가 반으로 줄어듬 -> 시간복잡도
- 이진 탐색
이진 탐색(binary search): 배열의 중앙에 있는 값을 조사하여 찾고자 하는 항목이 왼쪽 또는 오른쪽 부분 리스트에 있는지를 알아내어 탐색의 범위를 반으로 줄임
- 이진 탐색을 적용하려면 탐색 전 반드시 배열이 정렬되어 있어야 함
- 데이터의 삽입이나 삭제가 빈번한 경우보다 고정된 데이터에 대한 탐색에 더 적합함
<알고리즘 12.3.2.1> 순환 호출을 사용하는 이진 탐색
search_binary(list, low, high){
middle <- low에서 high 사이의 중간 위치
if( 탐색 값 = list[middle])
return TRUE;
else if( 탐색 값 < list[middle])
return list[low] 부터 list[middle-1]에서의 탐색;
else if( 탐색 값 > list[middle])
return list[middle+1] 부터 list[high]에서의 탐색;
}<프로그램 12.3.2.1> 재귀 호출을 이용한 이진 탐색
int search_binary(int key, int low, int high){
int middle;
if(low<=high){ // 아직 숫자가 남아 있는 경우
middle = low+high/2;
if(key == list[middle]) return middle; // 탐색 성공
else if(key < list[middle]) return search_binary(key, low, middle-1); // 왼쪽 부분 리스트
else return search_binary(key, middle+1, high); // 오른쪽 부분 리스트
}
return -1; // 탐색 실패
}<프로그램 12.3.2.2> 반복을 이용한 이진 탐색
int search_binary2(int key, int low, int high){
int middle;
while(low<=high){ // 아직 숫자들이 남아 있으면
middle = low+high/2;
if(key == list[middle]){
return middle; // 탐색 성공
}else if(key < list[middle]){
high = middle-1; // 왼쪽 부분 리스트
}else{
low = middle+1; // 오른쪽 부분 리스트
}
}
return -1; // 탐색 실패
}이진 탐색의 시간 복잡도
- 색인 순차 탐색
색인 순차 탐색(indexed sequential search): 인덱스(index)라 불리는 테이블을 사용하여 탐색의 효율을 높이는 방법
- 인덱스 테이블은 주자료 테이블에서 일정한 간격으로 발췌한 자료를 가지고 있음
- 인덱스 테이블에 m개의 항목이 있고, 주자료 테이블의 데이터 수가 n이면 각 인덱스 항목은 주자료 테이블의 각 n/m번째 테이터를 가리키고 있음
- 주 자료 테이블과 인덱스 테이블은 모두 정렬되어 있어야 함
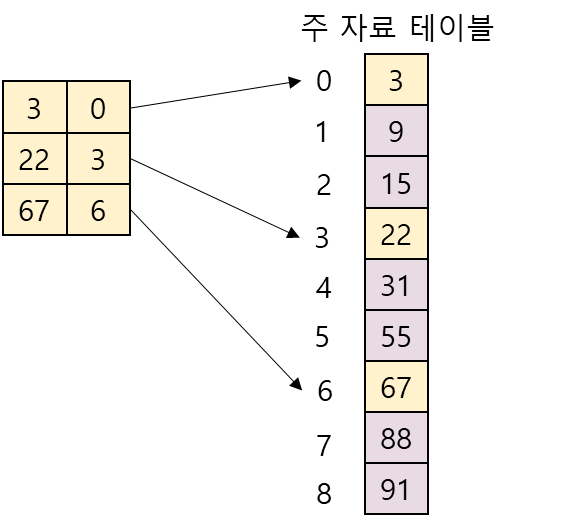
- 인덱스 테이블에서 index[i] <= key < index[i+1]을 만족하는 항목을 찾음
- 인덱스 테이블에서 위의 조건을 만족하는 항목으로부터 주 자료 테이블에서 순차 탐색을 수행
색인 순차 탐색 알고리즘을 위한 인덱스 테이블 구조체
typedef struct{
int key; // 인덱스가 가리키는 곳의 키 값 저장
int index; // 리스트의 인덱스 값 저장
} itable;
itable index_list[INDEX_SIZE];<프로그램 12.3.3.1> 색인 순차 탐색
// INDEX_SIZE는 인덱스 테이블의 크기, n은 전체 데이터의 수
int search_index(int key){
int i, low, high;
// 키 값이 리스트 범위 내의 값이 아니면 탐색 종료
if(key <list[0] || key > list[n-1])
return -1;
// 인덱스 테이블을 조사하여 해당 키의 구간 결정
for(i=0;i<INDEX_SIZE;i++){
if(index_list[i].key <= key && index_list[i+1].key > key){
break;
}
}
if(i==INDEX_SIZE){ // 인덱스 테이블의 끝이면
low = index_list[i-1].index;
high = n-1;
}else{
low = index_list[i].index;
high = index_list[i+1].index-1;
}
// 예상되는 범위만 순차 탐색
return seq_search(key,low,high);
}- 색인 순차 탐색 알고리즘의 탐색 성능은 인덱스 테이블 크기에 좌우됨
- 인덱스 테이블 크기를 줄이면 주 자료 테이블에서의 탐색 시간이 증가되고, 인덱스 테이블 크기를 크게하면 인덱스 테이블의 탐색 시간을 증가시킴
- 인덱스 테이블 크기가 m이고, 주 자료 테이블 크기가 n일 떄 시간복잡도는 과 같음
- 보간 탐색
보간 탐색(interpoliation search): 사전이나 전화번호부를 탐색하는 방법과 같이 탐색 키가 존재할 위치를 예측하여 탐색하는 방법
탐색 위치 결정 방법
->
-> k는 찾고자 하는 키 값, low와 high는 각각 탐색할 범위의 최소와 최대 인덱스 값
-> 위의 식은 탐색 위치를 결정할 때 찾고자하는 키 값이 있는 곳에 근접하게 되도록 가중치를 주는 것

ex) 3, 9, 15, 22, 31, 55, 67, 88, 89, 92로 구성된 리스트에서 탐색 구간이 0-9이고, 찾을 값이 55일 경우
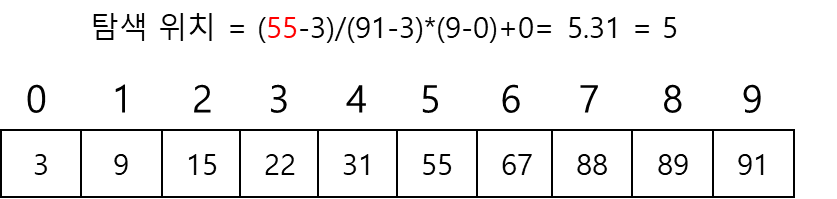
- 주의 할 점: 계산되어 나오는 값은 실수이며, 이 실수를 정수로 변환해주어야함(소수점 이하를 버리기)
<프로그램 12.3.4.1> 보간 탐색
int search_interpolation(int key, int n){
int low =0;
int high = n-1;
while((list[high] >= key) && (key > list[low])){
int j= ((float)(key-list[low])/(list[high]-list[low])*(high-low))+low;
if(key >list[j]) low = j+1;
else if(key <list[j]) high = j-1;
else low = j;
}
if(list[low] == key) return low; // 탐색 성공
else return -1; // 탐색 실패
}보간탐색의 시간복잡도
'자료구조와 알고리즘 ft. 수업 > 자료구조 정리' 카테고리의 다른 글
| 6. 보이어-무어 알고리즘 (0) | 2023.03.23 |
|---|---|
| 5. KMP 알고리즘 (0) | 2023.03.23 |
| 4. DFA 알고리즘 (0) | 2023.03.23 |
| 3. 카프-라빈 알고리즘 (0) | 2023.03.23 |
| 2. Naive 알고리즘 (고지식한 탐색 알고리즘) (0) | 2023.03.23 |
