Reference :
- 컴퓨터 구조 및 설계 MIPS EDITION [6판] / David A. Patterson / 한빛에듀
- 건국대학교 컴퓨터구조 강의 / 박능수 교수님
- https://developbear.tistory.com/ (김베어의 개발일지)
곱셈
먼저 곱셈 연산의 순서와 피연산자의 명칭을 확실히 해야한다.
0과 1로만 구성된 십진수의 곱셈, 1000×1001을 보자.
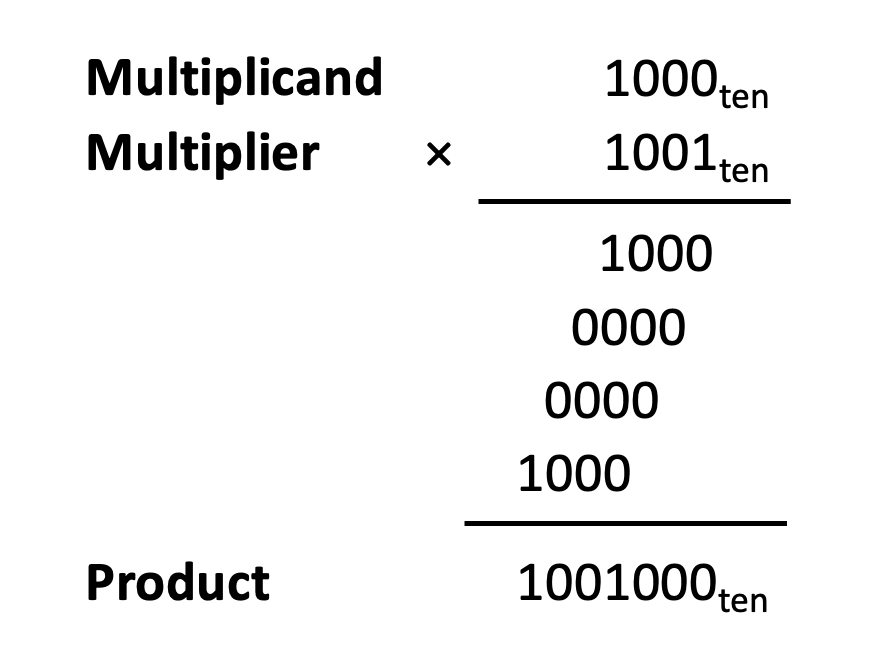
첫 번째 피연산자는 피승수(multiplicand),
두 번째 피연산자는 승수(multiplier)라고 부른다.
최종 결과는 곱(product)이라고 부른다.
이진수 곱셈은 위에서 본 예시와 같이, 다음과 같은 단계만 거치면 된다.
1. 승수의 자리 수가 1이면 피승수(1×피승수)를 해당 위치에 복사한다.
2. 승수의 자리 수가 0이면 0(0×피승수)을 해당 위치에 복사한다.

초기의 곱셈 하드웨어
초기에는 우리가 종이와 연필로 곱셈을 푸는 방법과 유사하게 하기 위해
데이터가 위에서 아래로 흐르도록 하였다.
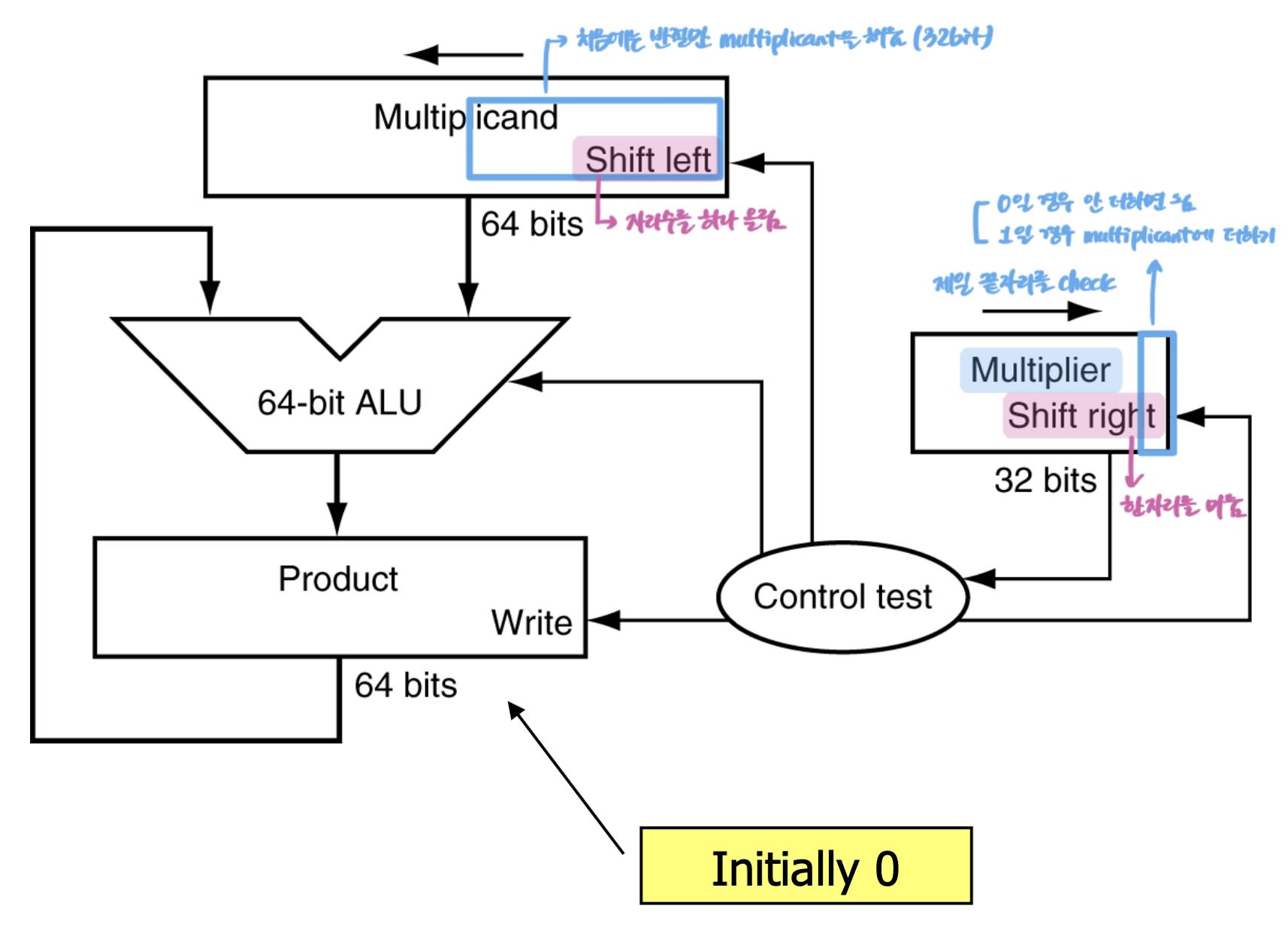
피승수(multiplicant) 레지스터, ALU, 곱(product) 레지스터는 모두 64비트이고,
승수(multiplier) 레지스터만 32비트이다.
64비트 곱(Product) 레지스터는 0으로 초기화되어 있다.
피승수(Multiplicant) 레지스터는 왜 64비트일까?
종이와 연필을 사용한 계산 방법대로라면, 매 단계마다 피승수는 왼쪽으로 한 자리씩 이동되어야 하고
필요하면 중간 결과에 더해주는 식으로 계산되어야 한다.
따라서 32단계를 거치면 32비트 피승수가 왼쪽으로 32번 이동하게 되는 것이기 때문에 64비트 피승수 레지스터가 필요한 것이다.
피승수 레지스터의 오른쪽 절반에는 32비트 피승수가 위치하고, 왼쪽 절반은 0으로 초기화된다.
64비트 곱 레지스터에 축적되는 합과 피승수의 위치를 맞추기 위해서
피승수 레지스터는 매 단계마다 1비트 왼쪽으로 자리이동된다. (shift left)
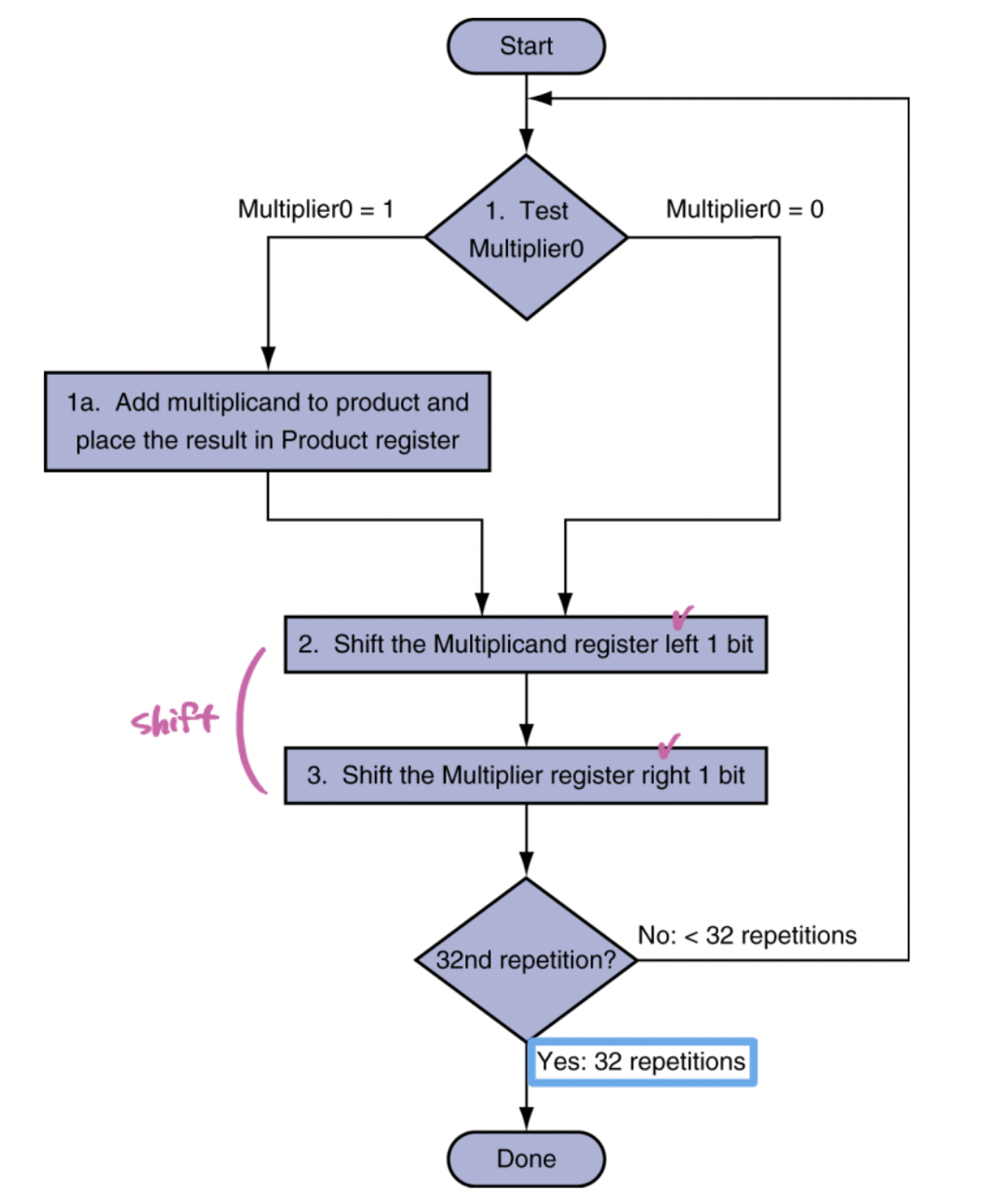
[ 단계 1 ]
승수의 최하위 비트(LSB)는 피승수를 곱 레지스터에 더할지 말지를 결정한다.
만약 LSB가 1이라면 피승수를 곱 레지스터에 더하게 되고, 0이라면 아무 연산도 하지 않는다.
[ 단계 2 ]
피승수 레지스터를 왼쪽으로 자리이동(shift left)하는 것은 피연산자를 왼쪽으로 이동시키는 역할을 한다.
[ 단계 3 ]
승수 레지스터를 오른쪽으로 자리이동(shift right)하는 것은 다음 번 반복에서 검사할 승수의 다음 비트를 준비하기 위해서이다.
최종 결과를 얻기 위해서는 이 세 단계를 32번 반복해야 한다.
32비트 숫자 두 개를 곱하는 데 거의 100개의 클럭 사이클이 걸린다.
또한, 덧셈기와 레지스터에서 사용되지 않는 부분이 존재한다.

따라서 덧셈기와 레지스터의 폭을 절반으로 줄여 더욱 최적화할 수 있다.
개선된 곱셈 하드웨어
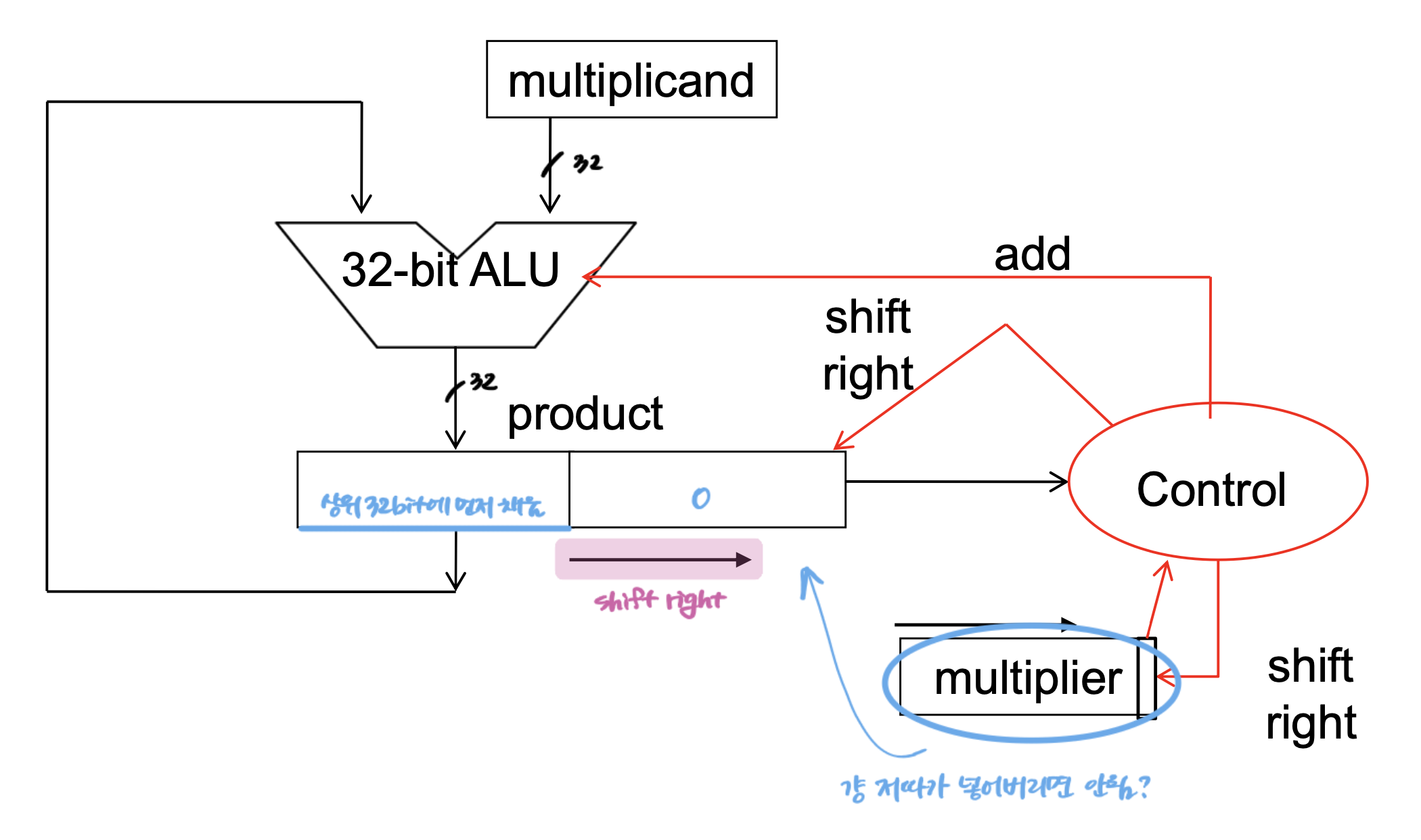
피승수(multiplicand) 레지스터, ALU, 승수(multiplier) 레지스터는 전부 32비트이고,
곱(product) 레지스터만이 64비트이다.
승수의 LSB가 1이면 피승수가 곱 레지스터의 상위 32비트에 더해지고,
이번에는 곱 레지스터가 오른쪽으로 자리이동(shift right)하며, 승수도 오른쪽으로 자리이동(shift right)한다.
곱 레지스터의 오른쪽 절반에 승수를 넣으면 공간의 낭비를 줄일 수 있다.
개선된 곱셈 하드웨어 (최종)
곱셈 하드웨어의 최종 버전은 다음과 같다.
예시로 0110(6)×0101(5)의 계산을 적어놓았으니, 찬찬히 보면서 과정을 이해하길 바란다.
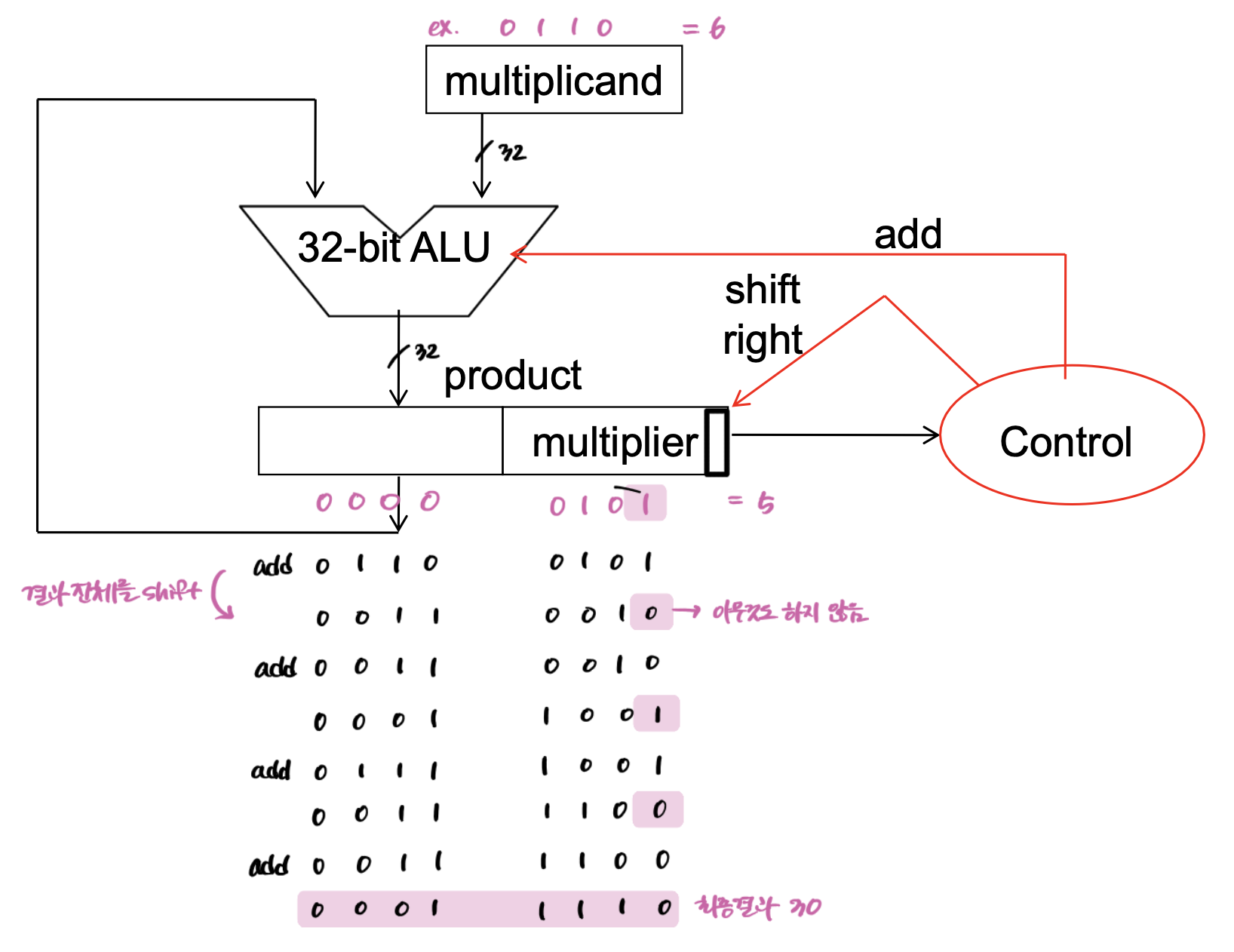
지금까지는 양수만을 다루었다.
부호있는 수의 곱셈은 어떻게 해야할까?
간단하게, 승수와 피승수를 모두 양수로 변환하고 31비트의 곱셉을 해준 다음
부호 판별만 해서 부호비트를 붙여주면 된다.
앞의 하드웨어에서는 하나의 덧셈기로 32번의 연산을 하였다.
그러나 아래 그림처럼 덧셈기를 32개 사용하여 병렬트리 구조를 만들면 log2(32) 즉, 5번의 덧셈 시간만 기다리면 된다.

즉, 더 많은 하드웨어를 사용하면 파이프라이닝을 통해 다수의 곱셈을 동시에 수행할 수 있어
병렬로 더 빠르게 연산을 할 수 있는 것이다.
MIPS 곱셈 명령어
MIPS 곱셈 명령어에는 mult와 multu가 있다.
mult $s0, $s1 # hi || lo = $s0 * $s1* hi : 수행 결과의 상위 32비트 / lo : 수행 결과의 하위 32비트
둘다 오버플로우를 무시하기 때문에 곱이 32비트에 들어갈 수 있을지 검사하는 것은 소프트웨어의 몫이다.
multu 수행 결과 hi가 0이거나
mult 수행 결과 hi가 lo의 부호와 같은 비트 32개로 채워져 있다면 오버플로우가 아니다.
오버플로우를 탐지하기 위해 hi를 범용 레지스터로 보내는데 mfhi(move from hi) 명령어를 사용할 수 있다.
mfhi rd # move from hi
mflo rd # move from lo'컴퓨터 구조 > Ch3. 컴퓨터 연산' 카테고리의 다른 글
| 6. 부동 소수점 반올림과 근사 (5) | 2023.05.02 |
|---|---|
| 5. 부동소수점 (0) | 2023.04.12 |
| 4. 나눗셈 (0) | 2023.04.11 |
| 2. 덧셈과 뺄셈 (0) | 2023.04.11 |
| 1. 서론 (0) | 2023.04.11 |
