2. 균형 이진 탐색 트리
균형 이진 탐색 트리
이진 탐색 ve 이진 탐색 트리
이진 탐색 = 자료들이 배열에 저장되어 있으므로 삽입과 삭제가 힘듦.(즉, 자료 삽입, 삭제시 앞 뒤의 원소를 이동시켜야함)
이진 탐색 트리 = 비교적 빠른 시간 안에 삽입과 삭제를 끝마칠 수 있는 구조
- 이진 탐색 트리에서는 균형을 유지하는 트리라면 탐색 연산은 의 시간복잡도를 가지지만, 균형 트리가 아닐 경우에는 로 시간복잡도가 높아지게 됨
- 이진 탐색 트리에서 균형을 유지하는 것이 중요함
-> 스스로 균형 트리를 만드는 AVL 트리가 존재함(상당히 복잡하므로 주제 전체를 다루지 않음)
1) AVL 트리
AVL 트리: Adelson-Velskii와 Landis에 의해 제안된 트리로서 각 노드에서 왼쪽 서브 트리의 높이와 오른쪽 서브 트리의 높이가 차이가 1이하인 이진 탐색 트리를 말함
AVL 트리는 트리가 비균형 상태가 되면 스스로 노드를 재배치하여 균형 상태로 만듦
-> AVL 트리는 균형 트리가 항상 보장되므로 탐색이 시간 안에 끝나게 됨 (+ 삽입, 삭제도 )
- 균형 인수(balance factor): 왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이
- 모든 노드의 균형 인수가 이하이면 AVL 트리

AVL 트리의 탐색 연산
AVL 트리도 탐색에서는 일반 이진 탐색 트리의 탐색 연산과 동일 -> 시간복잡도
AVL 트리의 삽입 연산
- 균형을 이루던 이진 탐색 트리에서 균형이 깨지는 이유는 삽입, 삭제 연산 때문
- 삽입 연산은 삽입되는 위치에서 루트까지의 경로에 있는 조상 노드들의 균형 인수에 영향을 줄 수 있음
- 새로운 노드가 삽입된 후 불균형 상태로 변한 가장 가까운 조상 노드(균형 인수가 가 된 가장 가까운 조상 노드)의 서브 트리들에 대해 다시 균형을 잡아야 함
-> 해결방법: 새로운 노드 부터 균형 인수가 가 된 가장 가까운 조상 노드까지 회전시키는 것
AVL 트리에서 균형이 깨지는 경우(4가지)
1. LL 타입: N(새로 삽입된 노드)이 A(가장 가까우면서 균형 인수가 가 된 조상 노드)의 왼쪽 서브 트리의 왼쪽 서브 트리에 삽입됨
2. RR 타입: N이 A의 오른쪽 서브 트리의 오른쪽 서브 트리에 삽입됨
3. RL 타입: N이 A의 오른쪽 서브 트리의 왼쪽 서브 트리에 삽입됨
4. LR 타입: N이 A의 왼쪽 서브 트리의 오른쪽 서브 트리에 삽입됨
재균형시키는 방법
1. LL 회전: A부터 N까지의 경로 상의 노드들을 오른쪽으로 회전시킴
2. RR 회전: A부터 N까지의 경로 상의 노드들을 왼쪽으로 회전시킴
3. RL 회전: A부터 N까지의 경로 상의 노드들을 오른쪽-왼쪽으로 회전시킴
4. LR 회전: A부터 N까지의 경로 상의 노드들을 왼쪽-오른쪽으로 회전시킴
- 단순 회전(single rotation): 한 번만 회전시키는 것 (ex) LL회전, RR회전) -> 탐색 순서를 유지하면서 부모와 자식 원소의 위치를 교환하면 됨
- 이중 회전(double rotation): 두 번의 회전이 필요한 것(ex) LR회전, RL회전)
LL 회전

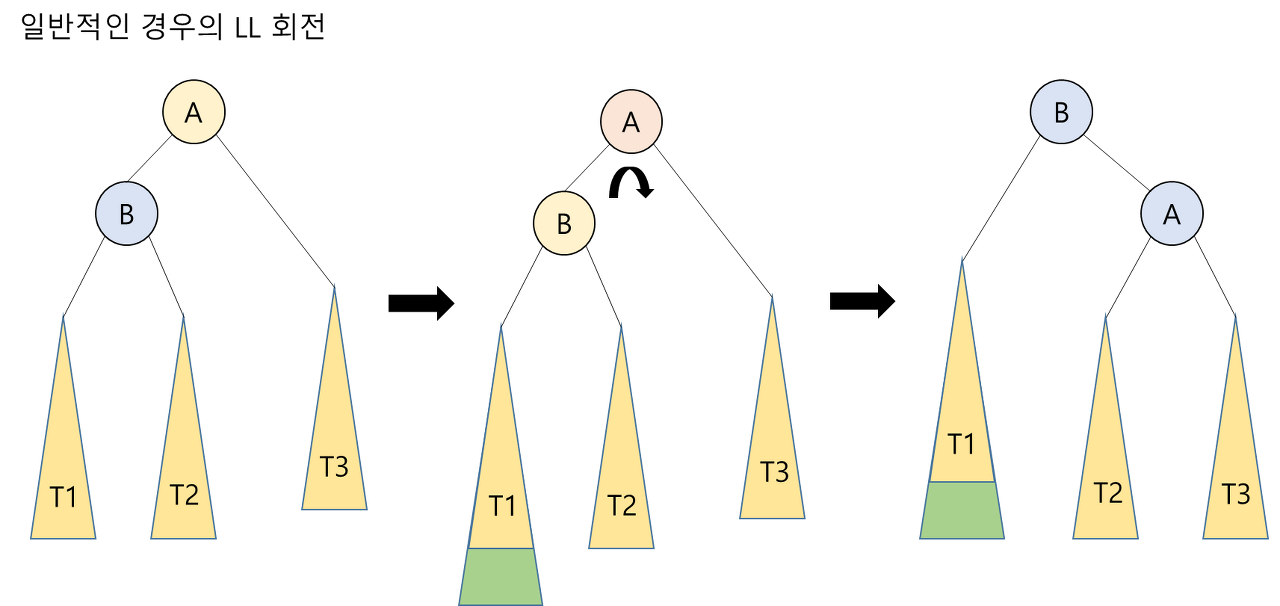
RR 회전
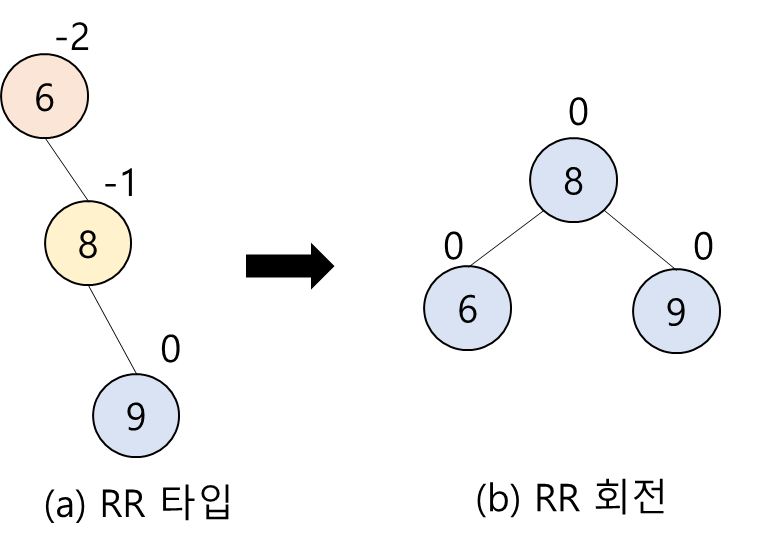

<알고리즘 12.4.1.1> AVL 트리에서의 단순 회전 알고리즘
rotate_LL(A)
B의 오른쪽 자식을 A의 왼쪽 자식으로 만듦
A를 B의 오른쪽 자식 노드로 만듦
rotate_RR(A)
B의 왼쪽 자식을 A의 오른쪽 자식으로 만듦
A를 B의 왼쪽 자식 노드로 만듦RL 회전
- RL 타입은 조상 노드 A의 오른쪽 서브 트리의 왼쪽 서브 트리에 노드가 추가됨으로써 발생
- RL 회전은 LL 회전을 한 다음, RR 회전을 하면 됨
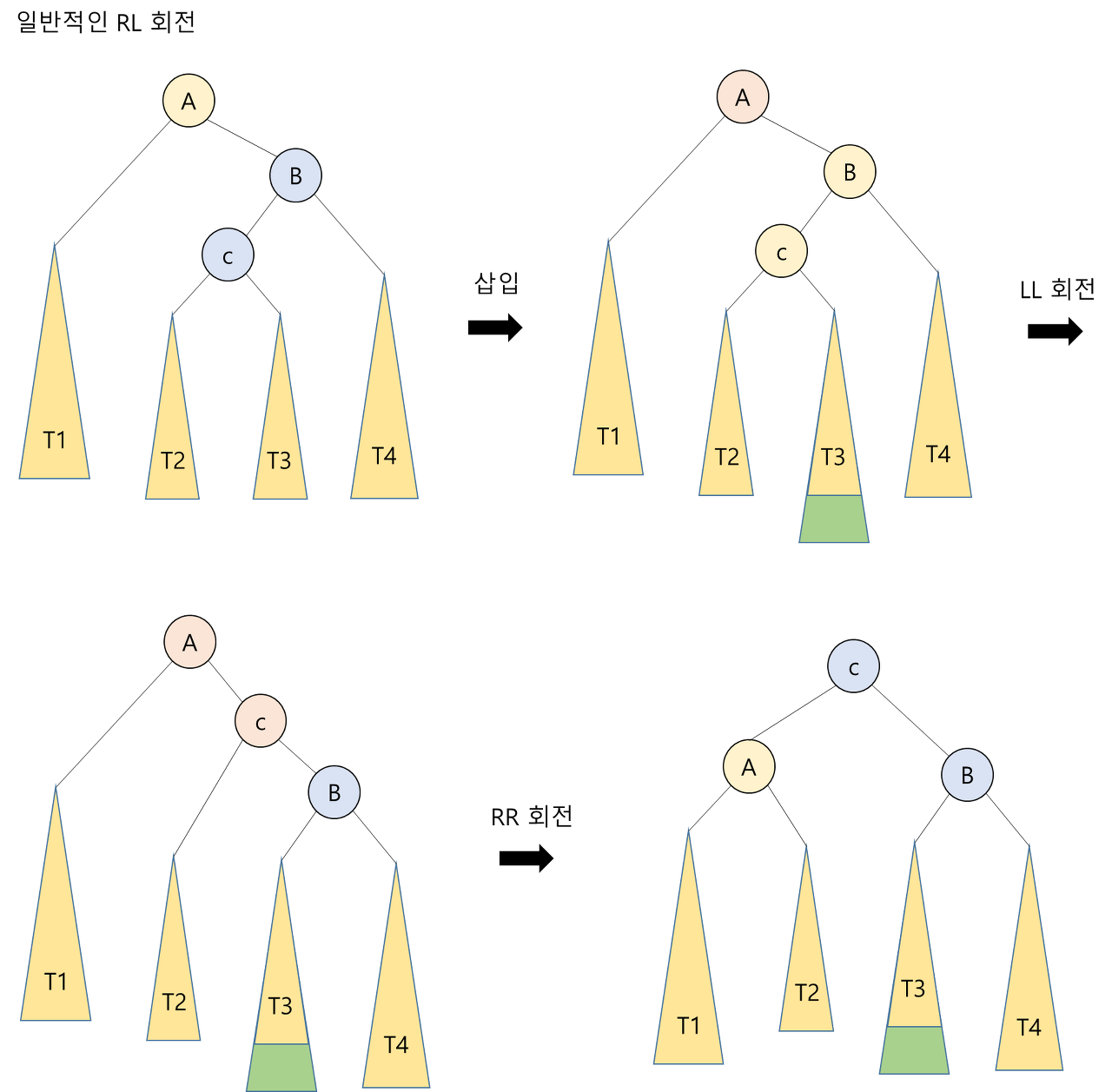
LR 회전
- LR 타입은 조상 노드 A의 왼쪽 서브 트리의 오른쪽 서브 트리에 노드가 추가됨으로써 발생
- LR 회전은 RR 회전을 한 다음, LL 회전을 하면 됨

<알고리즘 12.4.1.2> AVL 트리에서의 이중 회전 알고리즘
rotate_RL(A)
rotate_LL(B)가 반환하는 노드를 A의 오른쪽 자식으로 만듦
rotate_RR(A)
rotate_LR(A)
rotate_RR(B)가 반환하는 노드를 A의 왼쪽 자식으로 만듦
rotate_LL(A)ex) 7, 8, 9, 2, 1, 5, 3, 6, 4 데이터가 주어졌을 때, AVL 트리 구축 예)
삽입되는 노드: 주황색 / 위치가 변경되는 노드: 노란색

<프로그램 12.4.1.1> AVL 트리 구현 #1
- AVL 트리도 이진 탐색 트리의 일종
typedef struct AvlNode{
int data;
struct AvlNode *left_child, *right_child; // 왼쪽과 오른쪽 자식을 가리키는 포인터
}AvlNode;
AvlNode *root;<프로그램 12.4.1.2> AVL 트리 구현 #2
- LL 회전과 RR 회전은 루트와 자식을 바꿔주고 링크들을 수정하면 됨
- RL 회전과 LR 회전은 LL 회전 함수와, RR 회전 함수를 이용하여 구현됨
// LL 회전
AvlNode * rotate_LL(AvlNode *parent){
AvlNode *child = parent->left_child;
parent->left_child = child->right_child;
child->right_child = parent;
return child;
}
// RR 회전
AvlNode * rotate_RR(AvlNode *parent){
AvlNode *child = parent->right_child;
parent->right_child = child->left_child;
child->left_child = parent;
return child;
}
// RL 회전
AvlNode * rotate_RL(AvlNode *parent){
AvlNode *child = parent->right_child;
parent->right_child = rotate_LL(child);
return rotate_RR(parent);
}
// LR 회전
AvlNode * rotate_LR(AvlNode *parent){
AvlNode *child = parent->left_child;
parent->left_child = rotate_RR(child);
return rotate_LL(parent);
}<프로그램 12.4.1.3> AVL 트리 구현 #3
- 트리의 높이를 측정하는 함수(7장에 나옴): 루트에서 왼쪽 서브 트리와 오른쪽 서브 트리에 대해 각각 순환 호출을 하여 각각의 높이를 구한 다음, 이들 중에서 더 큰 값에 1을 더하면 트리의 높이가 됨
- 균형 인수 구하는 함수: 각각의 서브 트리에 대해 높이를 구한다면, 왼쪽 서브 트리의 높이에서 오른쪽 서브 트리의 높이를 뺴면 됨
// 트리의 높이를 반환
int get_height(AvlNode *node){
int height =0;
if(node !=NULL){
height = 1+ max(get_height(node->left_child), get_height(node->right_child));
}
return height;
}
// 노드의 균형 인수 반환
int get_height_diff(AvlNode *node){
if(node == NULL) return 0;
return get_height(node->left_child) - get_height(node->right_child);
}<프로그램 12.4.1.4> AVL 트리 구현 #4
- 트리를 균형으로 만들어주는 함수
- 양쪽 서브 트리의 높이의 차이(균형 인수)를 구한 다음
- 왼쪽 서브 트리가 더 높으면 왼쪽 서브 트리의 높이의 차이를 다시 구함(오른쪽 서브 트리가 높은 경우도 마찬가지)
- 여기에 따라 LL 회전인지, LR 회전인지 결정하고 해당 함수를 호출(RR 회전인지, RL 회전인지 결정하고 해당 함수 호출)
// 트리를 균형 트리로 만듦
AvlNode * rebalance(AvlNode **node){ // node가 포인터의 포인터가 된 이유는 node의 값이 함수 내에서 변경되어야 하기 때문
int height_diff = get_height_diff(*node);
if(height_diff > 1){
if(get_height_diff((*node)->left_child) > 0){
*node = rotate_LL(*node);
}else{
*node = rotate_LR(*node);
}
}else if(height_diff < -1){
if(get_height_diff((*node)->right_child) < 0){
*node = rotate_RR(*node);
}else{
*node = rotate_RL(*node);
}
}
return *node;
}<프로그램 12.4.1.5> AVL 트리 구현 #5
- 삽입 함수
- root가 NULL이면 현재 삽입하려는 탐색 키가 트리에 존재하지 않은 것이므로 탐색이 실패한 위치가 탐색 키를 삽입할 위치가 됨
- 동적 메모리 할당으로 새로운 노드를 만들어 root 포인터가 새로운 노드를 가리키도록하고 새로운 노드를 가리키는 포인터를 반환
- 만약, 현재 노드 값보다 탐색 키가 작을 경우 왼쪽 서브 트리를 대상으로 삽입 함수를 순환 호출함(클 경우 오른쪽 서브 트리 순환 호출, 같을 경우 탐색 키 중복으로 오류를 출력하고 복귀)
- 순환 호출이 끝나면 트리의 균형 상태를 만들기 위해 균형화 함수인 rebalance 함수를 호출
// AVL 트리의 삽입 연산
AvlNode *avl_add(AvlNode **root, int new_key){
if(*root == NULL){
*root = (AvlNode *)malloc(sizeof(AvlNode));
if(*root == NULL){
fprintf(stderr,"Memory allocate error\n");
exit(1);
}
(*root)->data = new_key;
(*root)->left_child = (*root)->right_child = NULL;
}else if(new_key < (*root)->data){
(*root)->left_child = avl_add(&((*root)->left_child), new_key);
*root = rebalance(root);
}else if(new_key > (*root)->data){
(*root)->right_child = avl_add(&((*root)->right_child), new_key);
*root = rebalance(root);
}else{
fprintf(stderr,"duplicate error\n");
exit(1);
}
return *root;
}<프로그램 12.4.1.6> AVL 트리 구현 #6
// AVL 트리의 탐색 함수
AvlNode *avl_search(AvlNode *node, int key){
if(node == NULL) return NULL;
printf("%d ",node->data);
if(key == node->data) return node;
else if(key < node->data) return avl_search(node->left_child, key);
else return avl_search(node->right_child, key);
}
int main()
{
// 8,9,10,2,1,5,3,6,4,7,11,12
avl_add(&root1, 8);
avl_add(&root1, 9);
avl_add(&root1, 10);
avl_add(&root1, 2);
avl_add(&root1, 1);
avl_add(&root1, 5);
avl_add(&root1, 3);
avl_add(&root1, 6);
avl_add(&root1, 4);
avl_add(&root1, 7);
avl_add(&root1, 11);
avl_add(&root1, 12);
printf("#1: ");
avl_search(root1, 12);
printf("\n");
// 7,8,9,2,1,5,3,6,4
avl_add(&root2, 7);
avl_add(&root2, 8);
avl_add(&root2, 9);
avl_add(&root2, 2);
avl_add(&root2, 1);
avl_add(&root2, 5);
avl_add(&root2, 3);
avl_add(&root2, 6);
avl_add(&root2, 4);
printf("#2: ");
avl_search(root2, 4);
printf("\n");
}
2) 2-3 트리
2-3 트리: 차수가 2 또는 3인 노드를 가지는 트리
- 삽입, 삭제 알고리즘이 AVL 트리보다 간단
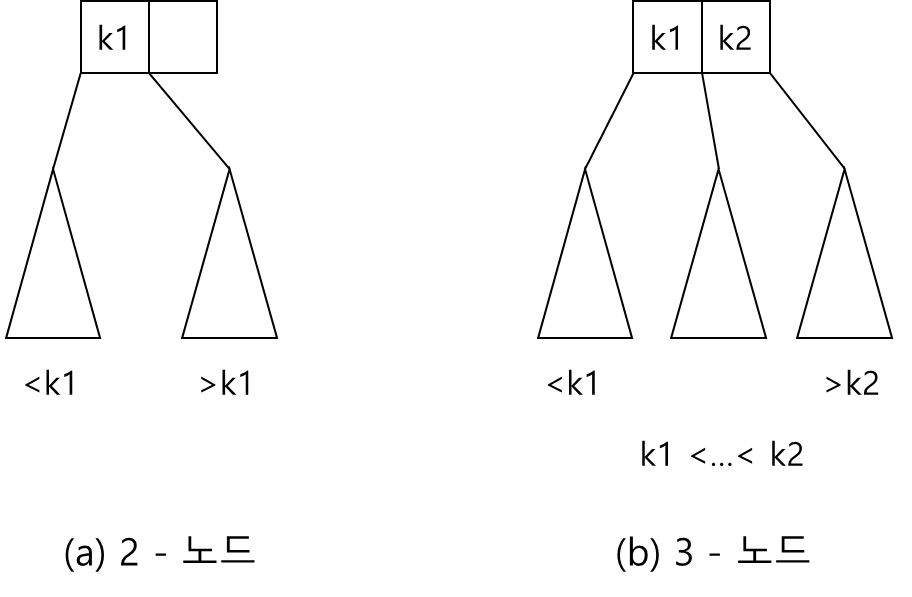
- 2-노드: 일반 이진 탐색 트리처럼 1개의 데이터 k1과 2 개의 자식 노드를 가짐
- 3-노드: 2개의 데이터 k1, k2와 3개의 자식 노드를 가짐 -> 왼쪽 서브 트리에 있는 데이터들은 모두 k1보다 작은 값, 중간 서브 트리에 있는 값들은 k1보다 크고, k2보다 작음, 오른쪽에 있는 데이터들은 모두 k2보다 큼
2-3 트리의 탐색 연산
int tree23_search(Tree23Node *root, int key){
if(root == NULL){ // 트리가 비어 있으면
return FALSE:
}else if(key == root.key1){ // 루트의 키 == 탐색 키
return TRUE;
}else if(root->type == TWO_NODE){ // 2-노드
if(key <root->key1){
return tree23_search(root->left, key);
}else{
return tree23_search(root->right, key);
}
}else{ // 3-노드
if(key <root->key1){
return tree23_search(root->left, key);
}else if(key > root->key1){
return tree23_search(root->right, key);
}else{
return tree23_search(root->middle, key);
}
}
}2-3 트리의 삽입 연산 리스트 ADT의 구현
- 2-3 트리의 노드는 2개의 데이터 값을 저장할 수 있음
- 2-3 트리에 데이터 추가 시에 노드에 추가할 수 있을 때까지 데이터는 추가되고 더 이상 저장할 장소가 없는 경우에는 노드를 분리하게 됨
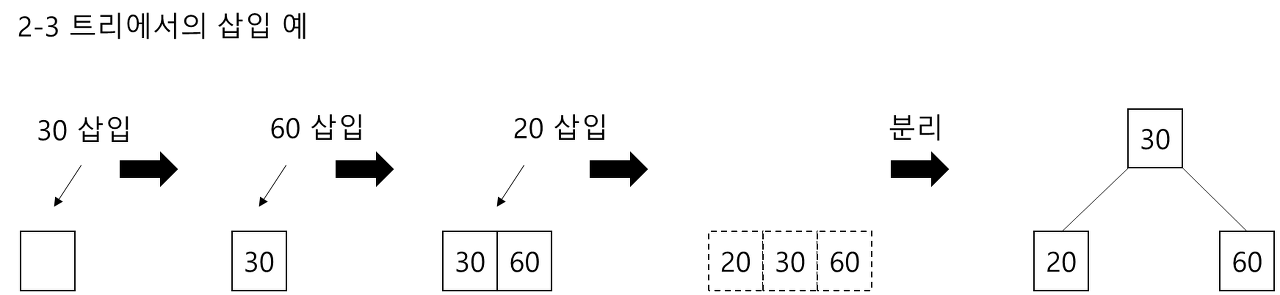
- 단말 노드를 분리하는 경우
- 단말 노드가 이미 2개의 데이터를 가지고 있는데 새로운 데이터가 삽입되어야 한다면 단말 노드는 분리되어야 함
- 부모 노드가 2-노드일 경우, 새로운 노드와 기존의 2개의 노드 중 중간 값을 부모의 노드로 올리고, 작은 값과 큰 값은 새로운 노드로 분리되게 됨
- 부모 노드가 이미 2개의 데이터를 가지고 있는 3-노드의 경우 부모 노드가 다시 분리되어야 함 -> 비단말 노드 분리
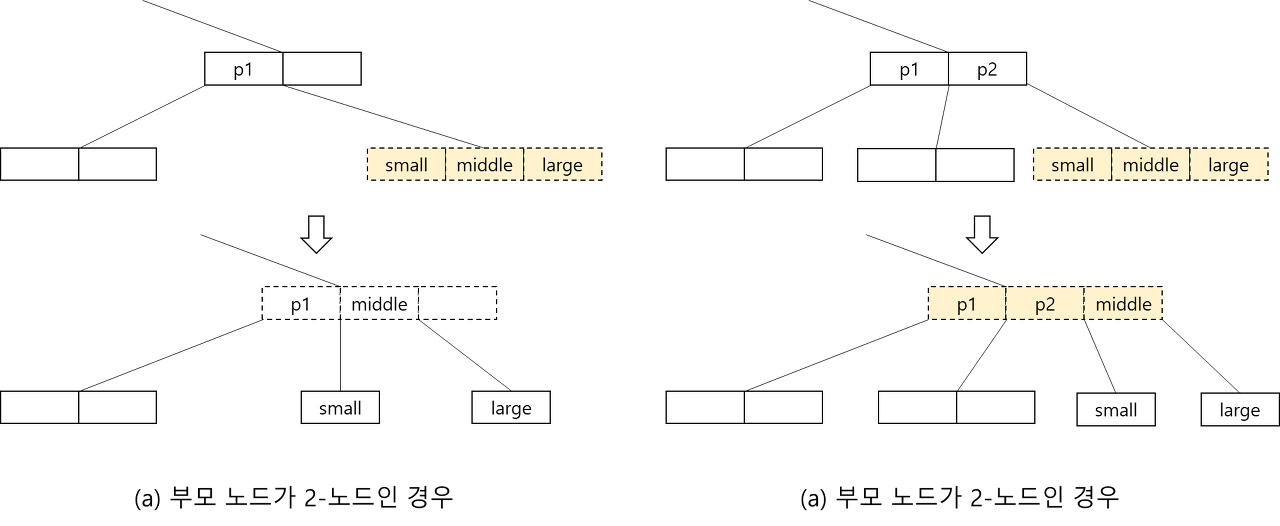
- 비단말 노드를 분리하는 경우
- 여기도 마찬가지로 중간 값을 다시 부모 노드로 올려보내고 작은 값과 큰 값을 별개의 노드로 분리
- 만약 다시 부모 노드에 추가 노드를 받을만한 공간이 없다면 다시 이러한 분리 과정이 부모 노드에 대해 되풀이 됨
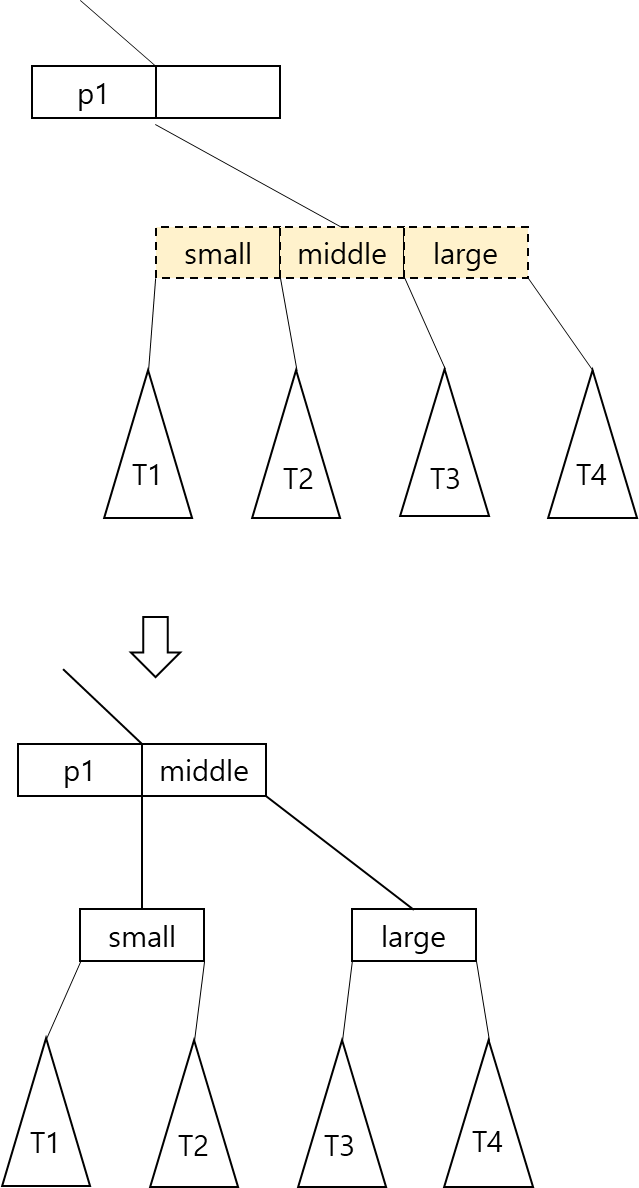
- 루트 노드를 분리하는 경우
- 루트 노드를 분리하게 되면 새로운 노드가 한 생기게 되므로 트리의 높이가 하나 증가하게 됨
- 새로 만들어지는 노드는 이 트리의 새로운 루트 노드가 됨
- 2-3 트리에서 높이가 증가하게 되는 것이 이 경우 뿐임
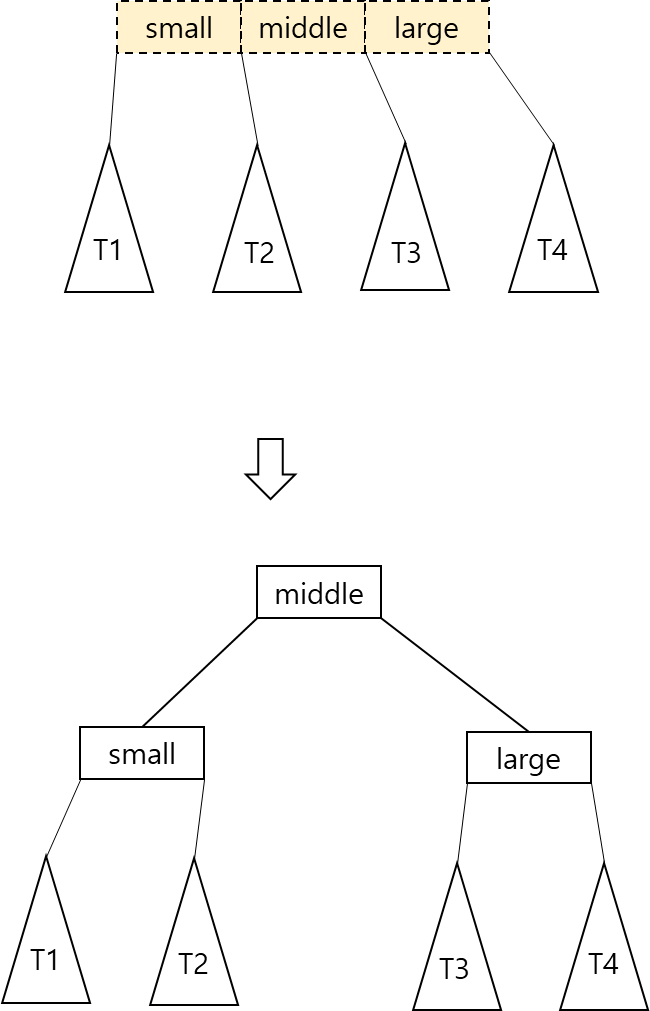
- 단말 노드를 분리하는 경우
3) 2-3-4 트리
2-3-4 트리: 하나의 노드가 4개의 자식까지 가질 수 있도록 2-3트리를 확장한 것
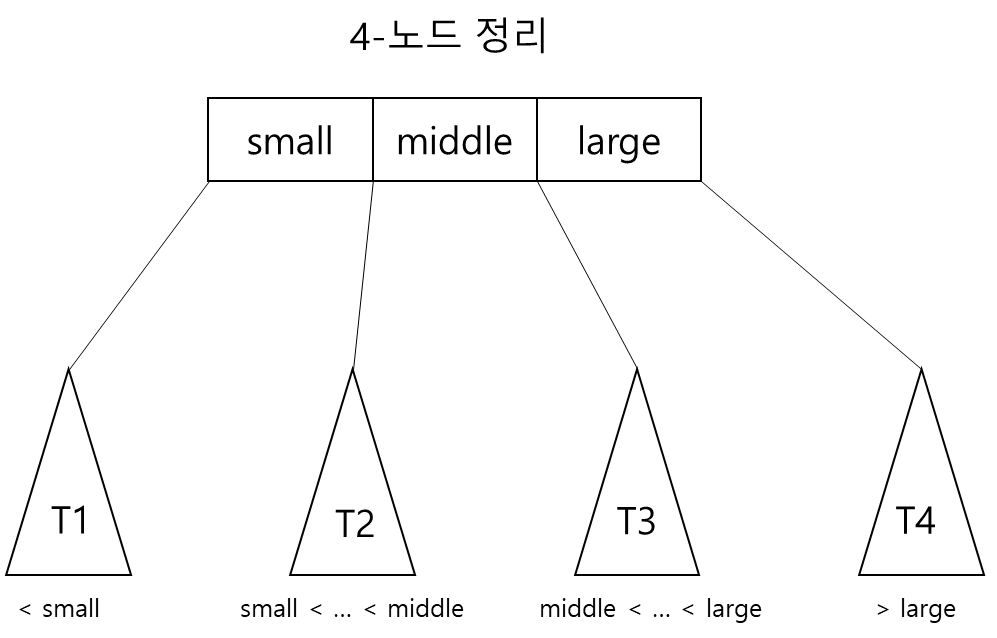
- 2-3-4 트리를 탐색하는 것은 2-3 트리의 탐색 알고리즘에 4-노드를 처리하는 부분만 추가하면 됨
2-3-4 트리의 삽입 연산
- 삽입해야 할 단말 노드가 2,3-노드인 경우 간단하게 삽입만 하면 됨
- 삽입해야 할 단말 노드가 4-노드인 경우 후진 분할(backward split)이 일어나게 됨 -> 이를 방지하기 위해 삽입 노드를 찾는 순회(루트->단말)시 4-노드를 만나면 미리 분할, 단말 노드에 도달했을 때 단말 노드의 부모 노드가 4-노드가 아니라는 것을 보장함
2-3 트리는 삽입 또는 삭제를 위한 순회와 분할, 합병의 영향으로 인한 순회가 필요함
-> 따라서, 2-3-4 트리의 장점은 순회를 한 번에 삽입 삭제가 가능하다는 것
- 4-노드가 루트인 경우
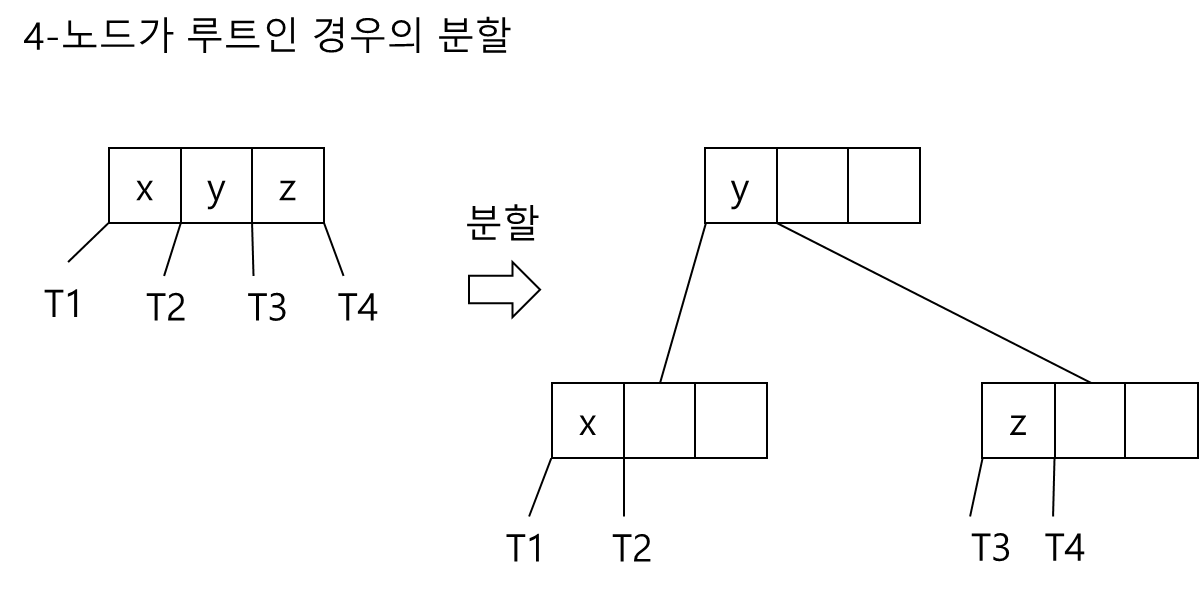
- 4-노드의 부모가 2-노드인 경우

- 4-노드의 부모가 3-노드인 경우